Java数据结构梳理

[TOC]

线性结构

线性结构特点

线性结构为最常用的数据结构，其特点是数据元素均为一对一的结构特点，即一个元素最多只有唯一后继，有且只有唯一前驱
线性结构有两种存储结构：
1. 顺序存储（数组） ---> 物理位置和逻辑位置是连续的
2. 链式存储（链表） ---> 物理位置不是连续的
线性结构对于检索的效率很低【数组，链表】

稀疏数组

稀疏数组介绍：当一个数组的大部分元素为0或为同一个值时，则若全部记录只会造成存储的数据大量的冗余，此时可以采用稀疏数组的存储方式进行存储
稀疏数组的处理方法：
1. 记录数组中不同值的个数以及数组的行数和列数
2. 将不同值元素的行列值记录在一个表内，从而缩小数组的规模

```java package LinearStruct;

import java.io.FileInputStream; import java.io.FileNotFoundException; import java.io.FileOutputStream; import java.io.IOException; import java.io.ObjectInputStream; import java.io.ObjectOutputStream;

import org.junit.jupiter.api.Test;

public class SparseMatrix {

static int matrix[][] = new int[3][3]; static { matrix[0][0] = 1; matrix[2][2] = 2; }

static public int[][] constrMatrix() { int cnt = 0; for(int i = 0;i < matrix.length;i++) for(int j = 0;j < matrix[0].length;j++) if(matrix[i][j] != 0)cnt++; int sparse[][] = new int[cnt + 1][3]; int index = 1;

  sparse[0][0] = 3;
  sparse[0][1] = 3;

  for(int i = 0;i < matrix.length;i++)
      for(int j = 0;j < matrix[0].length;j++)
          if(matrix[i][j] != 0) {
              sparse[index][0] = i;
              sparse[index][1] = j;
              sparse[index][2] = matrix[i][j];
              index++;
          }
  for(int i = 1;i <= cnt;i++)
      System.out.println(sparse[i][0] + " " + sparse[i][1] + " " + sparse[i][2]);

  System.out.println();
  return sparse;

}

static public void returnMatrix(int [][]sparse) { int row = sparse[0][0]; int col = sparse[0][1];

  int mat[][] = new int[row][col];
  for(int i = 1;i < sparse.length;i++) 
      mat[sparse[i][0]][sparse[i][1]] = sparse[i][2];



  for(int i = 0;i < mat.length;i++) {
      for(int j = 0;j < mat[0].length;j++)
          System.out.print(mat[i][j] + " ");
      System.out.println();
  }

}

static public void saveMatrix(int sparse[][]) { FileOutputStream fos = null; ObjectOutputStream oos = null;

  try {
      fos = new FileOutputStream("./mat.dat");
      oos = new ObjectOutputStream(fos);
      oos.writeObject(sparse);
  } catch (FileNotFoundException e) {
      // TODO Auto-generated catch block
      e.printStackTrace();
  } catch (IOException e) {
      // TODO Auto-generated catch block
      e.printStackTrace();
  }finally {
      try {
          fos.close();
          oos.close();
      } catch (IOException e) {
          // TODO Auto-generated catch block
          e.printStackTrace();
      }
  }

}

static public int[][] readMatrix(){ FileInputStream fis = null; ObjectInputStream ois = null; int sparse[][] = null;

  try {
      fis = new FileInputStream("./mat.dat");
      ois = new ObjectInputStream(fis);
      sparse = (int[][])ois.readObject();
  } catch (ClassNotFoundException | IOException e) {
      // TODO Auto-generated catch block
      e.printStackTrace();
  }finally {
      try {
          fis.close();
          ois.close();
      } catch (IOException e) {
          // TODO Auto-generated catch block
          e.printStackTrace();
      }
  }
  return sparse;

}

@Test public void test() { // returnMatrix(constrMatrix()); saveMatrix(constrMatrix()); returnMatrix(readMatrix()); }

}


  



#### 队列

- [ ] 队列为有序列表，可以用数组或链表来模拟实现
- [ ] 遵循先入先出的原则

##### 数组的队列模拟

- [ ] 数组模拟队列，即模拟的为有限队列，队列存在最大长度MaxSize

- [ ] 注意点

  - rear == MaxSize - 1时即队列已满
  - rear == head时队列为空
  - rear指向插入位置
  - head指向弹出位置

- [ ] ```java
  class ArrQueue{
  	int head = -1;
  	int rear = -1;
  	
  	int maxSize = 0;
  	int queue[] = null;
  	
  	public ArrQueue(int size) {
  		// TODO Auto-generated constructor stub
  		this.maxSize = size;
  		head = 0;
  		rear = 0;
  		queue = new int[size];
  	}
  	
  	public boolean isEmpty() {
  		if(this.queue == null || this.rear == this.head)return true;
  		else return false;
  	}
  	
  	public int length() {
  		return rear - head;
  	}
  	
  	public int top() {
  		if(!this.isEmpty()) 
  			return queue[head];
  		else {
  			System.out.println("empty queue!");
  			return -1;
  		}
  	}
  	
  	private boolean isFull() {
  		if(this.rear == this.maxSize -1)return true;
  		else return false;
  	}
  	
  	public int pop() {
  		if(!this.isEmpty())return this.queue[head++];
  		else{
  			System.out.println("empty queue");
  			return -1;
  		}
  	}
  	
  	public void push(int element) {
  		if(!this.isFull())
  			queue[rear++] = element;
  		else
  			System.out.println("full queue");
  		
  	}
  	
  	public Iterator iterator() {
  		Iterator it = new MyIterator();
  		return it;
  	}
  	
  	class MyIterator implements Iterator{
  		int start = head;
  		@Override
  		public boolean hasNext() {
  			// TODO Auto-generated method stub
  			if(start == rear)return false;
  			else return true;
  		}
  		@Override
  		public Object next() {
  			// TODO Auto-generated method stub
  			return queue[start++];
  		}
  		
  		
  	}
  	
  	
  	
  }

缺陷：
- 不能充分利用数组的空间，pop后的位置无法再使用
解决方法：
- 构造循环队列

数组循环队列

循环队列的构建方法：
- head ---> 指向队首
- rear ---> 指向将要push的位置，即空位置
- 此构建方法使得空出一个位置作为操作位，即无法push和pop的位置（真正的队尾位置）
- rear永远指向队列的空位置
判断依据：
- 当 rear == head 队列为空
- 当 (rear + 1) % MaxSize == head 队列为满【假的满队列，最后一个位置无法利用】
- 队列的元素个数：((rear + MaxSize) - head) % MaxSize

```java class CircleQueue{ int head = -1; int rear = -1; int queue[] = null; int maxSize = 0; public CircleQueue(int size) { // TODO Auto-generated constructor stub this.maxSize = size; queue = new int[size]; this.head = 0; this.rear = 0; }

public boolean isEmpty() { if(rear == head)return true; return false; }

public boolean isFull() { if(((rear + 1) % this.maxSize) == head)return true; else return false; }

public int pop() { int value = 0; if(!this.isEmpty()) { value = queue[head]; head = (head + 1) % this.maxSize; return value; } else { System.out.println("queue empty!"); return -1; }

}

public int top() { if(this.isEmpty()) { int value = this.queue[head]; head = (head + 1) % this.maxSize; return value; } else { System.out.println("empty queue"); return -1; } }

public void push(int element) { if(!this.isFull()) { queue[rear] = element; rear = (rear + 1) % this.maxSize; } else { System.out.println("full queue!");

}

public Iterator iterator() { return new MyIterator(); }

class MyIterator implements Iterator{ int start = head; @Override public boolean hasNext() { // TODO Auto-generated method stub if(rear == start)return false; else return true; } @Override public Object next() { // TODO Auto-generated method stub int value = queue[start]; start = (start + 1) % maxSize; return value; } }

}


  

#### 链表

- [ ] 链表介绍：

  - 链表是以结点的方式进行存储的，每个结点包含data域和next域
  - 链表的各个结点并**不一定**是连续存放的
  - 链表区分带头节点和不带头节点的链表
- [ ] 头节点介绍：

  - 不存放具体数据
  - 作用就是表示链表的头部
- [ ] 在使用头节点的链表时，一般将头节点和Node结点分开两个类，而不是统一一个类进行操作

  - head ----> SingleLinkedList
  - node ----> Node
- [ ] 注意问题：
  - 对于有head的结点注意在add和delete时更新方式
  - 对于有rear的结点注意在什么时候更新rear(循环链表，双向循环链表)

 ```mermaid
  classDiagram
  	SingleLinkedList <|-- Node1
  	SingleLinkedList : Node head
  	Node1 <|-- Node2
  	Node2 <|-- Node3
  	Node3 <|-- Node4

```java package LinearStruct;

import java.util.Iterator;

import org.junit.jupiter.api.Test;

public class List { @Test public void test() { SingleLinkedList list = new SingleLinkedList(); list.addIndex(3, "ych"); list.addIndex(1, "cqgg"); list.addIndex(10, "sss"); list.addIndex(0, "dwz");

  list.set(1, "sb");
  list.set(15, "666");
  list.delete(20);
  list.delete(10);
  list.delete(1);
  list.delete(0);
  list.delete(3);

  Iterator iterator = list.iterator();
  while(iterator.hasNext())
      System.out.println(iterator.next());

}

} class SingleLinkedList{ Node head = null; Node rear = null;

public void delete(int no) { if(head == null)return; if(head.no == no) { head = head.next; return; }

  for(Node temp = head;temp.next !=  null;temp = temp.next) {
      if(temp.next.no == no) {
          temp.next = temp.next.next;
          return;
      }
  }
  System.out.println("not find");

}

public void set(int no,String name) { if(head == null)return;

  for(Node temp = head;temp != null;temp = temp.next)
      if(temp.no == no) {
          temp.name = name;
          return;
      }

  return;

}

public void addIndex(int no,String name) { if(head == null) { Node node = new Node(no, name); head = node; rear = node; } else { Node node = new Node(no, name); if(no < this.head.no) { node.next = this.head; this.head = node; } else { Node temp = null; for(temp = head;temp.next != null;temp = temp.next) { if(no < temp.next.no) { node.next = temp.next; temp.next = node; return; } else continue; } temp.next = node; return; } } }

public void addRear(int no,String name) { if(head == null) { Node node = new Node(no, name); head = node; rear = node; } else { Node node = new Node(no, name); rear.next = node; rear = node; } }

public void addRearTrav(int no,String name) { if(head == null) { Node node = new Node(no, name); head = node; rear = node; } else { Node temp = null; temp = this.head; while(temp.next != null) temp = temp.next; Node node = new Node(no, name); temp.next = node; this.rear = node; } }

public Iterator iterator() { return new MyIterator();

} class MyIterator implements Iterator{

  Node front = head; 

  @Override
  public boolean hasNext() {
      // TODO Auto-generated method stub
      if(front != null)return true;
      else return false;
  }
  @Override
  public Object next() {
      // TODO Auto-generated method stub
      Object value = front;
      front = front.next;
      return value;
  }

}

class Node{

int no; String name; Node next = null; public Node(int no,String name) { // TODO Auto-generated constructor stub this.name = name; this.no = no; }

public String toString() { return no + " " + name; }

}


  

##### 链表注意点

- 在任何时刻都需要首先考虑头节点的问题

- 在**插入和删除时，temp结点踩到的永远是已经考虑过的结点**，此时需要考虑的是next结点，所以当temp.next == null时所以的结点就均被考虑过了，**而对于修改操作，temp踩到的点为未考虑过的点**，此时的全部考虑条件为temp == null，即对于增删操作需要找到其前一个点，而对于修改直接定位该点即可;

- 通过迭代器模式，更好的遍历结构体

- 被删除的结点无任何引用，会被JVM回收

  

##### 链表Question

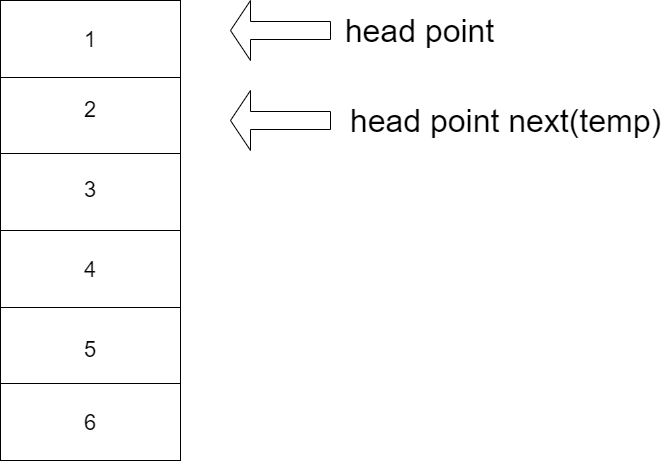
- [ ] 链表的快速反转（挤牙膏算法）

  - 基本思路：挤牙膏：
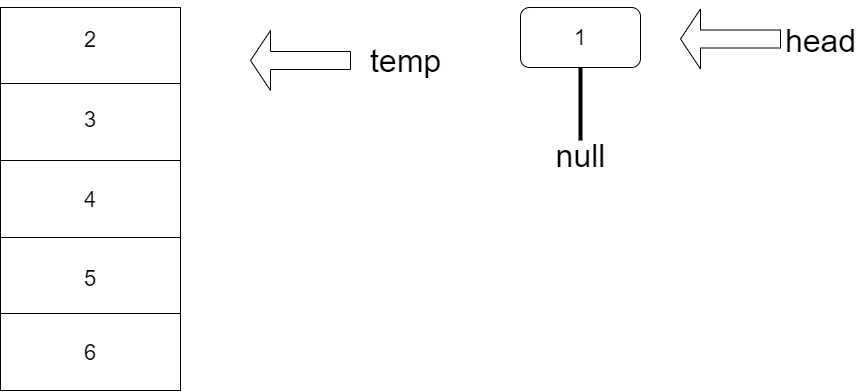
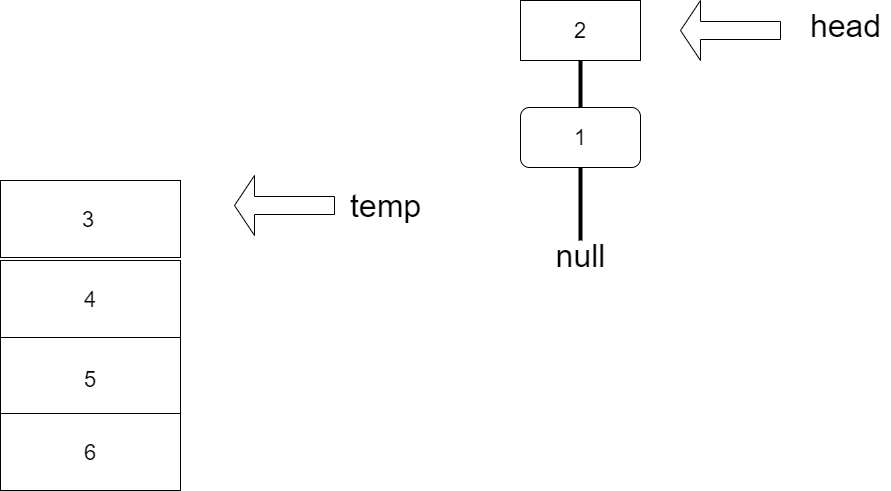
    1. 设置temp为牙膏管
    2. 每次从temp挤出一个node（注意第一个挤出的node的next设为null）
    3. 将node采用头插法插到head之前
    4. 完成反转
    
  - ![](/img/picLib/inverse.png)

  - ![](/img/picLib/未命名绘图.png)

  - ![](/img/picLib/inverse2.png)

  - ```java
    public void inverse() {
    		if(head == null || head.next == null)return;
    		
    		Node rear = head;
    		Node temp = head.next;
    		
    		rear.next = null;
    		
    		while(temp != null) {
    			Node node = temp;
    			temp = temp.next;
    			
    			node.next = head;
    			head = node;
    		}
    	}

实现单链表的反向输出：
- 方法一：先将链表反转，在进行正向输出（破坏了原有链表的结构，不建议）
- 方法二：利用栈，将哥哥结点压入栈

双向链表

对于每个结点都有两个指针：
- next ---> 指向后一个结点
- prior ---> 指向前一个结点

```java public void deleteDoubleList(int no) { if(no == head.no) { Node node = head.next; node.prior = null; head = node; return; } else { for(Node temp = head;temp.next != null;temp = temp.next) { if(no == temp.next.no) { temp.next = temp.next.next; if(temp.next != null)temp.next.prior = temp; return; } } } }

public void constrDoubleInTurn(int no,String name) { if(head == null) { Node node = new Node(no, name); head = node; node.next = null; node.prior = null; return; } else { Node node = new Node(no, name); if(no < head.no) { node.next = head; head.prior = node; head = node; rear = node; return; } else { Node temp = head; for(;temp.next != null;temp = temp.next) { if(no < temp.next.no) { node.next = temp.next; temp.next = node; node.prior = temp; node.next.prior = node; return; } } temp.next = node; node.prior = temp; rear = node;

      }
  }

}

public void constrDoubleList(int no,String name) { if(head == null) { Node node = new Node(no, name); head = node; node.next = null; node.prior = null; return; } else { Node node = new Node(no, name); Node temp = head; while(temp.next != null)temp = temp.next; temp.next = node; node.prior = temp; return;

}


  





##### 循环链表

- [ ] 对于list额外除了head外额外设置rear指针，且对于rear指针需要在add和delete额外进行判断

- [ ] ```java
  Node head = null;
  	Node rear = null;
  	
  	public void deleteCircle(int no) {
  		if(no == head.no) {
  			if(head.next == head)head = null;
  			else {
  				head = head.next;
  				rear.next = head;
  				
  			}
  		}
  		else {
  			Node temp = head;
  			for(;temp.next != head;temp = temp.next) {
  				if(no == temp.next.no) {
  					temp.next = temp.next.next;
  					if(temp.next == head)rear = temp;
  					return;
  				}
  			}
  		}
  		
  	}
  	
  	public void circleListInTurn(int no,String name) {
  		if(head == null) {
  			Node node = new Node(no, name);
  			node.next = node;
  			head = node;
  			rear = node;
  		}
  		else {
  			Node node = new Node(no, name);
  			if(no < head.no) {
  				node.next = head;
  				head = node;
  				rear.next = head;
  			}
  			else {
  				Node temp = head;
  				for(;temp.next != head;temp = temp.next) {
  					if(no < temp.next.no) {
  						node.next = temp.next;
  						temp.next = node;
  						return;
  					}
  				}
  				temp.next = node;
  				node.next = head;
  				rear = node;
  				
  			}
  		}
  			
  	}

约瑟夫环问题：
- 问题介绍：设置一个数m，一群人围城圈，从1开始依次报数，当报到m时，筛选出，下一个从1开始，以此类推，直到所有人退出
- 解决方法：通过循环链表，逐次delete结点，直到head == null结束

栈

数据结构特点：后入先出（LIFO）
栈中的特殊指针：
- 栈顶（Top）
- 栈底（Bottom）
- 元素的出入通过栈顶进行，栈底不变

数组模拟栈

```java class ArrayStack{ private int maxSize; private int []stack = null; private int top = -1;

public ArrayStack(int size) { // TODO Auto-generated constructor stub this.maxSize = size; stack = new int[size]; }

public boolean isFull() { return top == this.maxSize - 1; }

public boolean isEmpty() { return this.top == -1; }

public void push(int val) { if(!this.isFull()) { stack[++top] = val; } }

public int pop() { if(!this.isEmpty()) { return stack[top--]; } else throw new RuntimeException("stack empty!"); }

public Iterator iterator() { return new MyIterator(); }

class MyIterator implements Iterator{

  int start = top;
  @Override
  public boolean hasNext() {
      // TODO Auto-generated method stub
      return start != -1;
  }
  @Override
  public Object next() {
      // TODO Auto-generated method stub
      return stack[start--];
  }

}


##### 使用栈完成计算器

- [ ] 设置两个栈：
  - 数字栈
  - 符号栈
- [ ] 操作方式：
  - 如果是数字，直接压入数字栈
  - 如果是符号：
    1. 如果符号栈为空，直接进栈
    2. 如果符号优先级小于等于栈顶的符号使得优先级，则从数字栈中pop出两个数，从符号栈中pop出一个会数，进行计算，并将结果压入数字栈，将符号压入符号栈
       1. 如果当前的符号的优先级大于栈顶的符号优先级，符号直接入栈
  - 当扫描完毕，从数字栈和符号栈中pop出相应的数字和符号，并运行
  - 最后数字栈的结果就是计算结果





- [ ] ```mermaid
  classDiagram
  	Symbol <|-- NumSymbol
  	Symbol <|-- CalSymbol
  	
  	CalSymbol <|-- Add
  	CalSymbol <|-- Minus
  	CalSymbol <|-- Multipul
  	CalSymbol <|-- Division

- Symbol

package LinearStruct.Cal;

public interface Symbol {

}
package LinearStruct.Cal;

public abstract class CalSymbol implements Symbol,Comparable{
	int prior;
	
	@Override
	public int compareTo(Object o) {
		// TODO Auto-generated method stub
		CalSymbol symbol = (CalSymbol)o;
		if(this.prior < symbol.prior)return -1;
		else if(this.prior == symbol.prior)return 0;
		else return 1;
	}
	
	abstract public NumSymbol calculate(NumSymbol v1,NumSymbol v2);
	
}
package LinearStruct.Cal;

public class NumSymbol implements Symbol{
	int value;
	public NumSymbol(int val) {
		// TODO Auto-generated constructor stub
		this.value = val;
	}
	public String toString() {
		return String.valueOf(value);
	}

}
package LinearStruct.Cal;

public class Add extends CalSymbol{
	public Add() {
		// TODO Auto-generated constructor stub
		this.prior = 1;
	}
	
	@Override
	public NumSymbol calculate(NumSymbol v1, NumSymbol v2) {
		// TODO Auto-generated method stub
		return new NumSymbol(v1.value + v2.value);
	}
}
package LinearStruct.Cal;

public class Division extends CalSymbol{
	public Division() {
		// TODO Auto-generated constructor stub
		this.prior = 2;
	}
	
	@Override
	public NumSymbol calculate(NumSymbol v1, NumSymbol v2) {
		// TODO Auto-generated method stub
		return new NumSymbol(v1.value / v2.value);
	}

}
package LinearStruct.Cal;

public class Minus extends CalSymbol{
	public Minus() {
		// TODO Auto-generated constructor stub
		this.prior = 1;
	}
	@Override
	public NumSymbol calculate(NumSymbol v1, NumSymbol v2) {
		// TODO Auto-generated method stub
		return new NumSymbol(v1.value - v2.value);
	}
}
package LinearStruct.Cal;

public class Multipul extends CalSymbol{
	public Multipul() {
		// TODO Auto-generated constructor stub
		this.prior = 2;
	}
	@Override
	public NumSymbol calculate(NumSymbol v1, NumSymbol v2) {
		// TODO Auto-generated method stub
		return new NumSymbol(v1.value * v2.value);
	}
}

Client

package LinearStruct.Cal;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.Scanner;
import java.util.Stack;
import java.util.regex.Matcher;
import java.util.regex.Pattern;

public class Client {
	static public Pattern patternNum = Pattern.compile("[^0-9]");
	static public Pattern patternSym = Pattern.compile("//d*");
	static public Scanner sc = new Scanner(System.in);
	
	static public Pattern minus = Pattern.compile("-");
	static public Pattern add = Pattern.compile("//+");
	static public Pattern multipul = Pattern.compile("//*");
	static public Pattern division = Pattern.compile("/");
	static public HashMap<Pattern,Class> map = new HashMap<>();
	static {
		map.put(minus, Minus.class);
		map.put(add, Add.class);
		map.put(multipul, Multipul.class);
		map.put(division, Division.class);
	}
	
	static public int[] getNumArr(String str) {
		Matcher m = patternNum.matcher(str);
		String process = m.replaceAll(" ").trim();
		String numsStr[] = process.split(" ");
		int nums[] = new int[numsStr.length];
		for(int i = 0;i < numsStr.length;i++)
			nums[i] = Integer.parseInt(numsStr[i]);
		return nums;
	}
	
	static public String[] getSyms(String str) {
		Matcher m = patternSym.matcher(str);
		String syms[] = m.replaceAll(" ").replace(" ", "").split("");
		return syms;
	}
	
	static public CalSymbol consrtSym(String sym) throws InstantiationException, IllegalAccessException {
		for(Pattern p : map.keySet()) {
			Matcher m = p.matcher(sym);
			if(m.find())
				return (CalSymbol) map.get(p).newInstance();
		}
		return null;
	}
	
	static public String formatInput() {
		String input = sc.nextLine();
		String inputs[] = input.split("//s+");
		String res = "";
		for(String str : inputs)res += str;
		return res;
		
	}
	
	public static void main(String[] args) throws InstantiationException, IllegalAccessException {
		System.out.println("please input the expressionm : ");
		String input = formatInput();
		
		int nums[] = getNumArr(input);
		String syms[] = getSyms(input);

		
		Stack<NumSymbol> numStk = new Stack();
		Stack<CalSymbol> symStk = new Stack<CalSymbol>();
		
		ArrayList<Symbol> list = new ArrayList<>();
		ArrayList<NumSymbol> numList = new ArrayList<NumSymbol>();
		ArrayList<CalSymbol> symList = new ArrayList<CalSymbol>();
		
		for(Integer val : nums)
			numList.add(new NumSymbol(val));
		for(String str : syms) 
			symList.add(consrtSym(str));
		for(int i = 0;i < symList.size();i++) {
			list.add(numList.get(i));
			list.add(symList.get(i));
		}
		list.add(numList.get(numList.size() - 1));
		
	
		
		for(int i = 0;i < list.size();i++) {
			if(list.get(i) instanceof NumSymbol) {
				numStk.push((NumSymbol) list.get(i));
			}
			else {
				CalSymbol sym = (CalSymbol)list.get(i);
				if(symStk.isEmpty())symStk.push(sym);
				else {
					CalSymbol top = symStk.peek();
					if(sym.compareTo(top) > 0)symStk.push(sym);
					else {
						NumSymbol v1 = numStk.pop();
						NumSymbol v2 = numStk.pop();
						CalSymbol cal = symStk.pop();
						numStk.push(cal.calculate(v2, v1));
						symStk.push(sym);
					}
				}
			}
		}
		
		int epoch = symStk.size();
		for(int i = 0;i < epoch;i++) {
			NumSymbol v1 = numStk.pop();
			NumSymbol v2 = numStk.pop();
			CalSymbol cal = symStk.pop();
			numStk.push(cal.calculate(v2, v1));
		}
		
		
		System.out.println("result: " + numStk.pop());
		
		
	}

}

前缀 / 中缀 / 后缀表达式

前缀表达式（波兰表达式）

前缀表达式扫描顺序：从右至左，最右边为数字，最左边为符号

中缀表达式

最易人理解的表达式，但是不易计算机理解，原因是因为优先级的存在
在计算机计算时一般情况下将中缀表达式转化为后缀表达式

后缀表达式（逆波兰表达式）

后缀表达式扫描顺序：从左至右扫描，对应符号跟在数字之后

实现逆波兰计算器

```java package LinearStruct.ReversePolish;

import java.util.ArrayList; import java.util.Scanner; import java.util.Stack;

public class ReversePolishCal {

static public Scanner sc = new Scanner(System.in);

static public ArrayList<String> getList(String input){
    String strs[] = input.split(" ");
    ArrayList<String> list = new ArrayList<String>();
    for(String str : strs)
        list.add(str);
    return list;
}

static public void calPost(String input) {

    ArrayList<String> list = getList(input);
    Stack<String> stk = new Stack();

    for(String str : list) {
        if(str.matches("//d+"))stk.push(str);
        else {
            int v1 = Integer.parseInt(stk.pop());
            int v2 = Integer.parseInt(stk.pop());
            if(str.equals("+"))stk.push(String.valueOf(v2 + v1));
            else if(str.equals("-"))stk.push(String.valueOf(v2 - v1));
            else if(str.equals("*"))stk.push(String.valueOf(v2 * v1));
            else stk.push(String.valueOf(v2 / v1));
        }
    }


    System.out.println("result: " + stk.pop());
}

}

    
  
- [ ] 中缀表达式转后缀表达式

  - 步骤：

  > 1. 设置两个栈，一个为符号栈，一个为输出栈（即最终的后缀表达式的栈）
  > 2. 若遇到数字，则压入输出栈
  > 3. 若遇到符号：
  >    - 括号“（） ”不参与符号优先级比较
  >    - 符号栈顶为空，或符号栈顶为左括号，或优先级高于栈顶优先级，则压入符号栈
  >    - 若符号优先级小于符号栈顶的优先级，则将符号栈顶的符号弹至输出栈，并再次比较当前符号与新符号栈顶符号的优先级
  >    - 若遇到左括号，直接压入符号栈
  >    - 若遇到右括号，则依次弹出符号栈顶的符号，压入输出栈，直到遇到左括号，将左括号弹出丢弃，此时完成了一个括号的去除
  > 4. 最后将符号栈的元素依次弹出至输出栈
  > 5. 获得后缀表达式的逆序，再将表达式反转即得到最终会的后缀表达式

  - ```java
    package LinearStruct.ReversePolish;
    
    import java.util.ArrayList;
    import java.util.HashMap;
    import java.util.Scanner;
    import java.util.Stack;
    import java.util.regex.Matcher;
    import java.util.regex.Pattern;
    
    public class NifixToPost {
    	static public Scanner sc = new Scanner(System.in);
    
    	static public HashMap<String,Integer> map = new HashMap<>();
    	static {
    		map.put("+", 1);
    		map.put("-", 1);
    		map.put("*", 2);
    		map.put("/", 2);
    	}
    	
    	static public ArrayList<String> getList(String input) {
    		String all[] = input.split("");
    		ArrayList<String> list = new ArrayList<String>();
    		for(int i = 0;i < all.length;i++) {
    			if(all[i].matches("//d+")){
    				int j = i + 1;
    				String val = all[i];
    				while(j < all.length) {
    					if(all[j].matches("//d+"))val += all[j++];
    					else {
    						i = j - 1;
    						break;
    					}
    				}
    				list.add(val);
    			}
    			else list.add(all[i]);
    		}
    		
    		return list;
    	}
    	
    	
    	public static String formatInput() {
    		System.out.println("pleas input the expression: ");
    		String input = sc.nextLine();
    		String ins[] = input.split("//s+");
    		String res = "";
    		for(String str : ins)
    			res += str;
    		return res;
    	}
    
    	
    	public static void main(String[] args) {
    		String input = formatInput();
    		ArrayList<String> list = getList(input);
    		Stack<String> out = new Stack<String>();
    		Stack<String> symStk = new Stack<String>();
    //		System.out.println(3);
    		for(String str : list) {
    			if(str.matches("//d+")) out.push(str);
    			else {
    				if(symStk.isEmpty() || str.equals("("))symStk.push(str);
    				else {
    					if(str.equals(")")) {
    						while(true) {
    							String top = symStk.pop();
    							if(top.equals("("))break;
    							else out.push(top);
    						}
    					}
    					else {
    						String top = symStk.peek();
    						if(top.equals("(") || (map.get(str) > map.get(top)))symStk.push(str);
    						else {
    							while(true) {
    								String sym = symStk.peek();
    								if(symStk.isEmpty() || (map.get(str) > map.get(sym))) {
    									symStk.push(str);
    									break;
    								}
    								else out.push(symStk.pop());
    							}
    						}
    					}
    					
    				}
    			}
    		}
    //		System.out.println(6);
    		
    		while(!symStk.isEmpty())
    			out.push(symStk.pop());
    		
    		StringBuffer transVal = new StringBuffer();
    		while(!out.isEmpty())
    			transVal.append(out.pop() + " ");
    		
    		transVal = transVal.reverse();
    		String postVal = transVal.toString().trim();
    		
    		ReversePolishCal.calPost(postVal);
    		
    	}
    	
    	
    }

递归（Recursion）

介绍：
- 递归即函数自己调用自己，从而达到简化代码的结果
- 每次执行一个函数就会开辟一个栈区来存储局部变量
- 每个区域的变量是独立的
- 递归必须先考虑临界条件，否则容易造成栈溢出

迷宫问题

找到一条路（不一定是最短路，此处给出代码仅为普通递归（或者理解为dfs），而非bfs）

```java package LinearStruct.Recursion;

import org.junit.jupiter.api.Test;

public class Maze {

public int[][] way = null;
static public boolean flag = false;


public int[][] copy(int map[][]){
    int temp[][] = new int[8][7];

    for(int i = 0;i < map.length;i++)
        for(int j = 0;j < map[1].length;j++)
            temp[i][j] = map[i][j];
    return temp;
}

public void findWay(int map[][],int r,int c) {
    /* u up
     * d down
     * l left
     * r right
     * 
     * */

    System.out.println(r + " " + c);
    if(map[r + 1][c] == 6 || map[r - 1][c] == 6 || map[r][c + 1] == 6 || map[r][c - 1] == 6) {
        way = copy(map);
        flag = true;
        return;
    }
    else {
        if(map[r + 1][c] != 1 && map[r + 1][c] != 2 && !flag) {
            int temp[][] = copy(map);
            temp[r + 1][c] = 2;
            findWay(temp,r + 1,c);
        }

        if(map[r][c + 1] != 1 && map[r][c + 1] != 2 && !flag) {
            int temp[][] = copy(map);
            temp[r][c + 1] = 2;
            findWay(temp,r,c + 1);
        }

        if(map[r - 1][c] != 1 && map[r - 1][c] != 2 && !flag) {
            int temp[][] = copy(map);
            temp[r - 1][c] = 2;
            findWay(temp,r - 1,c);
        }


        if(map[r][c - 1] != 1 && map[r][c - 1] != 2 && !flag) {
            int temp[][] = copy(map);
            temp[r][c - 1] = 2;
            findWay(temp,r,c + 1);
        }
    }


}

@Test
public void test() {
    int map[][] = new int[8][7];
    for(int i = 0;i < 8;i++) {
        map[i][0] = 1;
        map[i][6] = 1;
        if(i <= 6) {
            map[0][i] = 1;
            map[7][i] = 1;
        }

    }
    map[3][1] = 1;
    map[3][2] = 1;
    map[3][3] = 2;
    map[6][5] = 6;
    for(int i = 0;i < 8;i++) {
        for(int j = 0;j < 7;j++)
            System.out.print(map[i][j] + " ");
        System.out.println();
    }
    findWay(map,3,3);

    for(int i = 0;i < 8;i++) {
        for(int j = 0;j < 7;j++)
            System.out.print(way[i][j] + " ");
        System.out.println();
    }

}


- [ ] 若要找到最短路需要使用bfs算法



##### 八皇后问题

- [ ] 问题介绍：

  - 8个皇后
  - 8 * 8棋盘

  - 对于所有的皇后不能在一条直线，一条竖线，一条对角线

- [ ] 基本思路：

  - 既然8*8棋盘，8个皇后，所以每个皇后必然独占一行，因此只需按照行进行递归判断即可
  - 基本思路依然为dfs

- [ ] ```java
  package LinearStruct.ReversePolish;
  
  import org.junit.jupiter.api.Test;
  
  public class EightQueens {
  	
  	static public int cnt = 0;
  	public void show(int map[][]) {
  		System.out.println("no." + cnt);
  		for(int i = 0;i < 8;i++) {
  			for(int j = 0;j < 8;j++)
  				System.out.print(map[i][j] + " ");
  			System.out.println();
  		}
  		System.out.println("-------------------------------" + "/n");
  	}
  	public void queens(int map[][],int row) {
  		if(row == 8) {
  			cnt++;
  			show(map);
  			return;
  		}
  		else {
  			for(int j = 0;j < 8;j++) {
  				for(int k = 0;k < 8;k++)
  					map[row][k] = 0;
  				
  				if(row == 0) {
  					map[0][j] = 1;
  					queens(map,row + 1);
  				}
  				else {
  					boolean flag = false;
  					for(int i = 0;i < row;i++)
  						if(map[i][j] == 1) {
  							flag = true;
  							break;
  						}
  					if(flag)continue;
  					for(int r = row - 1,init = j - 1;r >= 0 && init >= 0;r--,init--)
  						if(map[r][init] == 1) {
  							flag = true;
  							break;
  						}
  					for(int r = row - 1,init = j + 1;r >= 0 && init < 8;r--,init++)
  						if(map[r][init] == 1) {
  							flag = true;
  							break;
  						}
  					
  					if(flag)continue;
  					map[row][j] = 1;
  					queens(map,row + 1);
  					
  				}
  			}
  		}
  		
  	}
  	
  	
  	@Test
  	public void test() {
  		int map[][] = new int[8][8];	
  		queens(map,0);
  		System.out.println(cnt);
  	}
  }

排序算法

排序种类

内部排序：
- 数据量适中，可以一次性加载到内存进行排序
- 排序方法：
  1. 插入排序：
    1. 直接插入排序
    2. 希尔排序
  2. 选择排序
    1. 简单选择排序
    2. 堆排序
  3. 交换排序
    1. 冒泡排序
    2. 快速排序
  4. 归并排序
  5. 基数排序（桶排序）
  6. 堆排序【放在树中详述】
外部排序：
- 数据量过大无法全部加载到内存进行排序，需要借助外部存储进行排序

算法时间复杂度统计方法

事后统计法
- 在程序运行过后进行时间的统计
事前估计法
- 统计时间复杂度
- T(n) = O(n)【采用了极限的思想】：
  1. 忽略常数项
  2. 忽略低次项
  3. 忽略项系数
T(n) 为多项式表达式，f(n)为T(n)的同阶系数为1的单项式 ==》T(n) = O(f(n))

平均时间复杂度

最坏时间复杂度

算法在考虑时间复杂度时考虑最坏时间复杂度

冒泡排序

基本思想：
- 扫描序列，依次查看相邻的元素的值，如果出现逆序则进行交换，使较大的值移向尾部(由此看出冒泡排序是稳定的排序算法)
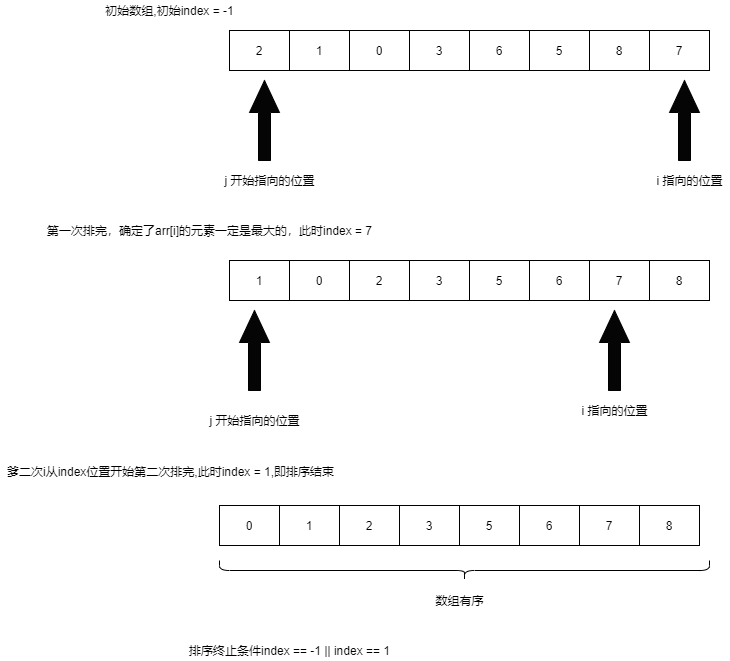
- 冒泡优化：当一趟扫描后从来未进行交换则说明已经有序，通过设置index位来标识是否进行排序，从而降低一定的时间复杂度
- 理解：
  1. i即外层指向的位置为此次排序一定能确定的位置
  2. j从0遍历到i - 1，若有逆序进行交换
  3. index确定上一次交换的位置，若无交换则为-1【index = -1表示数组有序，index = 1表示上一次交换的为第一个位置，交换后数组有序】，若index不为-1则i = index，下一次i从最后依次交换的位置开始
图解：

```java public class BubleSort {

//基本buble sort

static public void sort(int arr[]) {

  int cnt = arr.length - 1;
  for(int i = cnt;i >= 0;i--) {
      for(int j = 0;j < i;j++) 
          if(arr[j] > arr[j + 1]) {
              int temp = arr[j];
              arr[j] = arr[j + 1];
              arr[j + 1] = temp;
          }
  }

}

// 加如index后

static public void sortOpt(int arr[]) { int cnt = arr.length - 1; for(int i = cnt;i >= 1;i--) { int index = -1; for(int j = 0;j < i;j++) if(arr[j] > arr[j + 1]) { int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; index = j;

          }

      if(index == -1)break;
      else i = index + 1; //此处为index + 1 not index呦嘻嘻
  }

}


  



#### 选择排序

- [ ] 每次找到当前索引至数组尾部最小/最大的元素放在指定的位置

- [ ] 基本思想：

  - 每次确定arr[i]位置的元素
  - i 之前的位置均为已确定的元素
  - j从i + 1开始,只要arr[j] < arr[i]就交换两个位置上的元素

- [ ] 选择排序的不稳定性：

  ![](/img/picLib/selection.png)

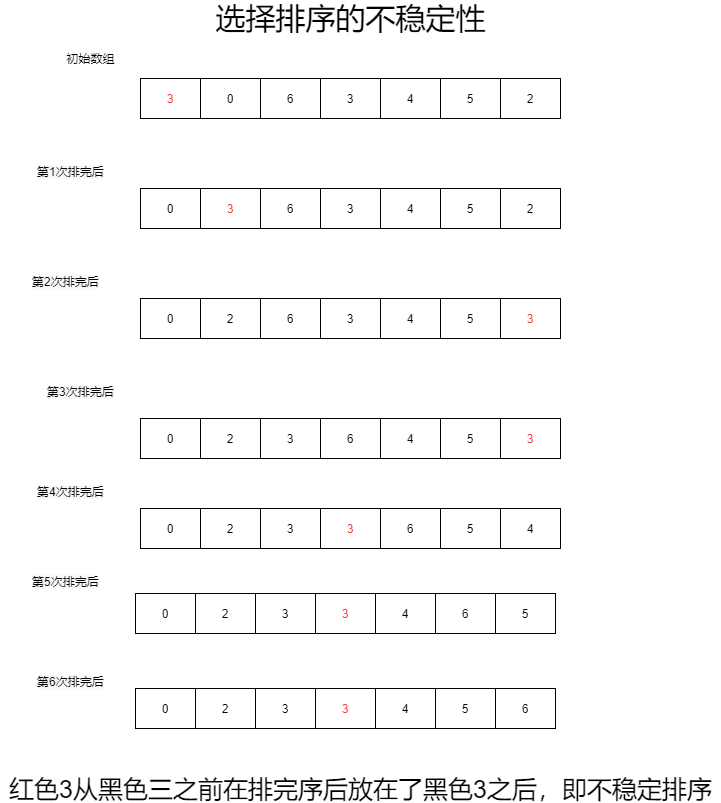
- [ ] ```java
  package SortAlgorithm;
  
  public class SelectionSort {
  	
  	static public void sort(int arr[]) {
  		for(int i = 0;i < arr.length;i++) {
  			for(int j = i + 1;j < arr.length;j++)
  				if(arr[j] < arr[i]) {
  					int temp = arr[j];
  					arr[j] = arr[i];
  					arr[i] = temp;
  				}
  			
  		}
  	}
  
  }

插入排序

基本介绍：
- 进行循环，在每一次循环在i之前的为有序列表，在之后的为无需列表
- 实则即为找到合适的位置进行交换元素,通过相邻交换的思想实现插入的方法
- 使得每一次使arr[i]的元素在其正确的位置

分类：

交换式

static public void sort(int arr[]) {
		for(int i = 1;i < arr.length;i++) {
			for(int j = i;j > 0;j--)
				if(arr[j] < arr[j - 1]) {
					int temp = arr[j];
					arr[j] = arr[j - 1];
					arr[j - 1] = temp;
				}
				else break;
		}
		
	}

移位式

static public void sortSwap(int arr[]) {
		for(int i = 1;i < arr.length;i++) {
			int temp = arr[i];
			int j = i;
			if(arr[j] < arr[j - 1]) {
				while(j - 1 >= 0 && temp < arr[j - 1]) {
					arr[j] = arr[j - 1];
					j -= 1;
					
				}
				arr[j] = temp;
				
			}
		}
	}

移位式排序算法要快于交换式的排序算法：移位的过程中只需要覆盖而不需要替换，而交换时的排序算法即需要进行覆盖也需要进行元素的替换
对于插入算法，不管是移位式还是交换式算法都是稳定的排序算法

插入排序缺点：
- 当插入的数较小时，需要多次的交换和比较

希尔排序

希尔排序也是一种插入排序，简单插入排序的优化算法，也称缩小增量排序
基本思想：
- 希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序
- 随着增量的减少每组包含的关键词增多，当增量减至1时，整个文件被分为1组，算法终止
- 即分组 + 插入排序

类型：

交换式

static public void sort(int arr[]) {
		int gap = arr.length / 2;
		for(;gap > 0;gap /= 2) {
			for(int i = gap;i < arr.length;i++) {
				for(int j = i - gap;j >= 0;j -= gap) {
					if(arr[j] > arr[j + gap]) {
						int temp = arr[j];
						arr[j] = arr[j + gap];
						arr[j + gap] = temp;
					}
				}
					
			}
				
		}
	}

移位式

static public void sortSwapShell(int arr[]) {
		for(int gap = arr.length / 2;gap > 0;gap /= 2) {
			for(int i = gap;i < arr.length;i++) {
				int temp = arr[i];
				int j = i;
				if(temp < arr[i - gap]) {
					while(j - gap >= 0 && temp < arr[j - gap]) {
						arr[j] = arr[j - gap];
						j -= gap;
					}
					arr[j] = temp;
						
				}
			}
		}
		
	}

移位式的平均排序速度要快于交换式

虽然希尔排序底层依然是插入排序但是插入排序是稳定的而希尔排序是不稳定的

快速排序

基本思想：
- 快排是对冒泡排序的一种改进
- 原理：
  1. 先经过一趟排序，将数组分成两部分，以一个数为基准，比一个数小的所有元素放在左侧，比一个数大的所有元素放在右侧
  2. 对左右两侧的元素递归的使用快速排序
  3. 即每次执行一遍sort至少 确定1/2的元素范围 + 1个确切的元素位置
- 主要：
  1. 设置每个数字的第一个元素为确定pos
  2. 为什么要确定第一个数？
    - 使得right--可以收敛【要么right < left，要么right == left（即第一个元素的位置已经对了）】
  3. 因为选择的最左端，所以利用right--进行收敛

```java package SortAlgorithm;

import java.util.Arrays;

public class QuickSort { // 2 1 5 2 6

static public void swap(int arr[],int pos1,int pos2) { int temp = arr[pos1]; arr[pos1] = arr[pos2]; arr[pos2] = temp;

} //2 1 5 2 6

static public int partation(int arr[],int left,int right) { int value = arr[left]; int l = left; int r = right + 1; while(true) { while(arr[++l] < value && l < right); while(arr[--r] > value && r > left); if(l < r) swap(arr,l,r); else break; } swap(arr,r,left); return r; }

// 在快排中一个重要的问题就是left和right是否可以取到！ // 另一个问题是对于重复元素的判断 static public void sort(int arr[],int left,int right) { if(left < right) { int pos = partation(arr, left, right);

      sort(arr,left,pos - 1);
      sort(arr,pos + 1,right);
  }
  else return;

} }


**上下对比【partation】**

- [ ] ```java
  
  	static public int partation(int arr[],int left,int right) {
  		int value = arr[right];
  		int l = left;
  		int r = right - 1;
  		while(true) {
  			while(l < right && arr[l] < value)l++;
  			while(r > left && arr[r] > value)r--;
  			if(l < r)
  				swap(arr,l,r);
  			else break;
  		}
  		swap(arr,l,right);
  		return l;
  	}

此方法与上面的方法进行对比可以发现，若设置左边为收敛位置，则需要使用右边进行默认的交换，反之，若要设置右边为收敛位置则需要左边为默认交换

归并排序

基本原理：
- 采用了分治策略:
  1. 分割数组
  2. 合并有序
- 分至末层，使得两个有序，再进行合并，合并有序序列
类型：
- 递归法
- 非递归法
- 递归和非递归思想均为分治策略，但是实际的逻辑顺序不同

```java package SortAlgorithm;

public class MergeSort {

static public void copy(int cpy[],int arr[],int left,int right) { int index = 0; for(int i = left;i <= right;i++) arr[i] = cpy[index++]; }

static public void merge(int arr[],int left,int mid,int right) { int copy[] = new int[right - left + 1]; int i = 0; int p1 = left; int p2 = mid + 1; while(p1 != mid + 1 && p2 != right + 1) { if(arr[p1] < arr[p2])copy[i++] = arr[p1++]; else if(arr[p1] >= arr[p2])copy[i++] = arr[p2++]; } if(p1 > mid) for(int p = p2;p <= right;p++) copy[i++] = arr[p]; else for(int p = p1;p <= mid;p++) copy[i++] = arr[p];

  copy(copy,arr,left,right);

}

static public void sort(int arr[],int left,int right) { if(left < right) { int mid = (left + right) / 2; sort(arr,left,mid); sort(arr,mid + 1,right); merge(arr,left,mid,right); } }

}


  





#### 基数排序（桶排序）

- [ ] 基本介绍：
  - 基数排序（radix sort）又称分配式排序（distribute sort）或桶排序（bucket sort）
  - 通过键值的各个位置的值，将要排序的元素分配至某些桶中去，从而达到排序的效果
  - 基数排序属于稳定的排序算法，且效率较高
  - 基数排序是桶排序的扩展
  
- [ ] 基本思想：
  - 将所有待比较的数统一为同样的数位长度，数位较短的数前面补0，然后从最低为开始，依次进行一次排列。这样从最低为排序到最高位排序以后，数列变为一个有序的数列
  
  - **典型的以空间换时间的算法**
  
  - 时间复杂度 ： n * maxLength
  
  - 优先级：
  
    1. 最高位的值
    2. 数值的位数
  
  - **基数排序不可进行含有负数的排序【缺点】**
  
    
  
- [ ] ```java
  package SortAlgorithm;
  
  import java.util.Arrays;
  
  public class RadixSort {
  	
  	static public void sort(int arr[]) {
  		StringBuilder nums[] = new StringBuilder[arr.length];
  		int maxLen = 0;
  		for (int i = 0; i < nums.length; i++) {
  			nums[i] = new StringBuilder(String.valueOf(arr[i])).reverse();
  			if(maxLen < nums[i].length())
  				maxLen = nums[i].length();
  		}
  		
  		StringBuilder bucket[][] = new StringBuilder[10][arr.length];
  		
  		int point = 0;
  		
  		while(point < maxLen) {
  			
  			int cnt[] = new int[10];
  			
  			for(StringBuilder num : nums)
  				if(num.length() > point) {
  					int pos = Integer.parseInt(String.valueOf(num.charAt(point)));
  					bucket[pos][cnt[pos]++] = num;
  				}
  				else bucket[0][cnt[0]++] = num;
  			
  			int index = 0;
  			System.out.println(Arrays.toString(cnt));
  			for(int i = 0;i <= 9;i++)
  				for(int j = 0;j < cnt[i];j++) 
  					nums[index++] = bucket[i][j];
  			point++;
  				
  		}
  		
  		for(int i = 0;i < arr.length;i++)
  			arr[i] = Integer.parseInt(String.valueOf(nums[i].reverse()));
  		
  		
  	}
  
  }

排序算法总结

[ ]	排序算法	平均时间复杂度	最好情况	最坏情况	空间复杂度	排序方式
冒泡排序	O(n^2)	O(n)	O(n^2)	O(1)	In-place	稳定
选择排序	O(n^2)	O(n^2)	O(n^2)	O(1)	In-place	不稳定
插入排序	O(n^2)	O(n)	O(n^2)	O(1)	In-place	稳定
希尔排序	O(n * log(n))	O(n * log^2(n))	O(n * log^2(n))	O(1)	In-place	不稳定
快速排序	O(n * log(n))	O(n * log(n))	O（n^2）	O(log(n))	In-place	不稳定
合并排序	O(n * log(n))	O(n * log(n))	O(n * log(n))	O（n）	Out-place	稳定
堆排序	O(n * log(n))	O(n * log(n))	O(n * log(n))	O(1）	In-pace	不稳定
基数排序	O(n * k)	O(n * k)	O(n * k)	O(n + k)	Out-place	稳定
桶排序	O(n + k)	O(n + k)	O(n^2)	O(n + k)	Out-place	稳定
计数排序	O(n + k)	O(n + k)	O(n + k)	O(k)	Out-place	稳定

相关术语：
- 稳定 / 不稳定
- 内排序 / 外排序：所有操作是否在内存中完成
- 时间复杂度/空间复杂度
- In-place / Out-place：是否占用额外的空间

查找算法

顺序查找
二分查找
插值查找
斐波那契查找
在以上所有的查找算法中只有顺序查找不要求数组有序，其余的算法均需要要求数列有序

顺序查找

原理：懂得都懂

```java package SearchAlgorithm;

public class SeqSearch {

static public int search(int arr[],int key) { for(int i = 0;i < arr.length;i++) if(arr[i] == key)return i; return -1; }

}


  





#### 二分查找

- [ ] 基本原理

  - 先决条件位数组必须是**有序数组，否则不能使用二分查找**
  - 分类：
    1. 递归式
    2. 迭代式
  - 注意点，left和right位置的元素是否可以取到

- [ ] ```java
  package SearchAlgorithm;
  
  public class BinarySearch {
  	
  	
  	static public int searchIterator(int arr[],int key,int left,int right) {
  		if(left <= right) {
  			while(left <= right) {
  				int mid = (left + right) / 2;
  				if(arr[mid] == key)return mid;
  				else if(arr[mid] > key)right = mid - 1;
  				else left = mid + 1;
  			}
  			return -1;
  		}
  		else return -1;
  	}
  	
  	
  	static public int searchRecursion(int arr[],int key,int left,int right) {
  		
  		if(left <= right) {
  			int mid = (left + right) / 2;
  			if(arr[mid] == key)return mid;
  			else {
  				if(arr[mid] > key)return searchRecursion(arr, key, left, mid - 1);
  				else return searchRecursion(arr, key, mid + 1, right);
  			}
  		}
  		else return -1;
  	}
  
  }

改进二分查找，查找所有的元素

static public void searchAll(int arr[],int key,int left,int right,HashSet pos) {
		if(left <= right) {
			int mid = (left + right) / 2;
			if(arr[mid] == key) {
				pos.add(mid);
				searchAll(arr,key,left,mid - 1,pos);
				searchAll(arr,key,mid + 1,right,pos);
			}
			else {
				if(arr[mid] > key)searchAll(arr, key, left, mid - 1,pos);
				else searchAll(arr, key, mid + 1, right,pos);
			}
		}
		
		
	}

插值查找

基本原理：
- 对于二分查找的改进版
- 也需要数组为有序数组
- 即将数组补充为fabnacci数组，通过找到分割点fab[k - 1] + 1的位置，判断在key和该点的关系，从而确定接下来的k值和要找的部位
改进部位：
对于二分查找：mid = low + 0.5 * (high - low)【这样忽略了key值对于查找的启发】

插值查找更像是二分查找的启发式查找：
- mid = low + (key - arr[low]) / (arr[high] - arr[low]) * (high - low)
- 从而体现了key值对于查找范围的启发
注意点：
- 因为为key - arr[left]，所有需要保证key大于左值
- 又因为需要乘积因子小于等于1，所以key小于等于右值

```java package SearchAlgorithm;

public class InterpolationSearch {

static public int search(int arr[],int key,int left,int right) { if(left <= right && key >= arr[left] && key <= arr[right]) { double coeffcient = (double)(key - arr[left]) / (double)(arr[right] - arr[left]); int pos = left + (int)(coeffcient * (right - left)); if(arr[pos] == key)return pos; else { if(arr[pos] > key)return search(arr, key, left, pos - 1); else return search(arr, key, pos + 1, right); }

  }
  else return -1;

}


- [ ] 与二分查找比较：

  - 对于数据量较大，关键字分布均匀使用插值查找效率要高于二分查找
  - 关键词分布不均匀的情况下可能不如二分查找



#### 斐波那契查找

- [ ] 基本原理：斐波那契查找，别名：黄金分割查找。

  - > 补充小知识：
    >
    > 对于斐波那契序列，相邻的两个值逐渐接近黄金分割数0.618,可以通过斐波那契数列计算黄金分割的近似值

  - 斐波那契查找也为改变coefficient值，从而完成有序数列的查找

  - 斐波那契查找也需要数组是有序数组

  - > **pos = low + fab[k - 1] - 1**

- [ ] ![](/img/picLib/fabs.png)

- [ ] ```java
  package SearchAlgorithm;
  
  import java.util.Arrays;
  
  public class FabonacciSearch {
  	
  	
  	static public int maxSize = 30;
  	
  	static public int[] getFabonacci() {
  		int arr[] = new int[maxSize];
  		arr[0] = 1;
  		arr[1] = 1;
  		for(int i = 2;i < 30;i++)
  			arr[i] = arr[i - 1] + arr[i - 2];
  		return arr;
  	}
  	
  	static public int search(int arr[],int key) {
  		int left = 0;
  		int right = arr.length - 1;
  		int k = 0;
  		int fabHeap[] = getFabonacci();
  		
  		while(right >= fabHeap[k] - 1)k++; //找到合适的k值
          
  		int temp[] = Arrays.copyOf(arr, fabHeap[k]);
  		
  		for(int i = right + 1;i < temp.length;i++) // 使用arr[right]进行填充空白区域
  			temp[i] = arr[right];
  		
  		while(left <= right) {
  			int pos = left + fabHeap[k - 1] - 1;
  			if(temp[pos] > key) { //在前一段
  				right = pos - 1;
  				k--;
  			}
  			else if(temp[pos] < key) { //在后一段
  				left = pos + 1;
  				k -= 2;
  			}
  			else {
  				if(pos <= right)return pos; //在补充部位
  				else return right;
  			}
  		}
  		return -1;
  		
  	}
  	
  	
  }

哈希表【非冲突消解】

基本概念：
- 根据关键码值而直接进行访问的数据结构，通过把关键码值进行映射到表中的一个位置来访问，从而加快访问记录，映射函数叫做散列函数
注意：
- HashTable实际上是二维的结构，因此在创建链表数组对象后需要动态的创建数组的每一个对象
- 哈希表实质上是数据结构的组合，利用数组进行哈希值处理，在相同HashCode基础上，再通过其他数据结构存储相同HashCode的元素，从而加快了查找的效率
- 采用上述方法即不用再使用冲突消解策略，当HashCode相同时采用高效的数据结构进行存储，优点是增加了代码的适用性，但是Hash查找的效率不是O(1)了，而是存储数据结构的效率

员工管理哈希

package HashTable;

import org.junit.jupiter.api.Test;

public class HashQuestion {
	
	@Test
	public void test() {
		HashManage manage = new HashManage(10);
		manage.addEmp(new Employee(0, "111"));
		Employee e = manage.searchByID(1);
		System.out.println(e);
	}
	
	
}
class Employee{
	int id;
	String name;
	boolean sex;
	String address;
	
	Employee next = null;;
	
	
	public Employee(int id,String name) {
		// TODO Auto-generated constructor stub
		this.id = id;
		this.name = name;
	}
	
	public String toString() {
		return "id: " + id + " name: " + name;
	}
	
	
	
}
class HashManage{
	EmpList hashTable[];
	int size;
	
	public HashManage(int size) {
		// TODO Auto-generated constructor stub
		hashTable = new EmpList[size];
		this.size = size;
		// 注意需要初始化每个位置的链表
		for(int i = 0;i < hashTable.length;i++)
			hashTable[i] = new EmpList();
	}
	
	public int hashFunc(Employee e) {
		return e.id % this.size;
	}
	
	public int hashFunc(int id) {
		return id % this.size;
	}
	
	public void addEmp(Employee e) {
		int pos = this.hashFunc(e);
		hashTable[pos].add(e);	
	}
	
	public Employee searchByID(int id) {
		int pos = this.hashFunc(id);
		Employee temp = hashTable[pos].head;
		while(temp != null)
			if(temp.id == id)return temp;
			else temp = temp.next;
		return null;
		
	}
	
}


class EmpList{
	Employee head = null;
	
	public void add(Employee e) {
		if(head == null)
			head = e;
		else {
			Employee temp = head;
			while(temp.next != null)temp = temp.next;
			temp.next = e;
		}
	}
	
	public void traverse() {
		Employee temp = head;
		while(temp != null) {
			System.out.println(temp);
			temp = temp.next;
		}
	}
}

树

树结构基础部分

此章所有代码均放在章节末BinaryTree中

树的基本术语

数组，链表，树分析

数组结构：
- 优点：
  1. 通过下标访问元素，速度快
  2. 对于有序数组，可以通过有序查找算法提高查找效率
- 缺点:
  1. 检索某一个值或者插入值需要指针对整个数组的移动，效率低
链表结构：
- 优点：
  1. 在一定程度上对数组的插入删除进行了优化
- 缺点：
  1. 检索效率依然很慢
数结构：
- 优点：
  1. 能提高数据的检索效率
  2. 既能保证插入删除的效率，又能保证检索的效率
- 缺点：
  1. 需要占用更大的存储空间

二叉树

基本概念

每个节点最多只能有两个子节点，且子节点分为左右子节点
若每层均满，则n层共有2^(n） - 1个节点，第n层有2^(n - 1)个
如果所有的叶子节点均在最后一层，则该二叉树称为满二叉树
完全二叉树：
- 所有的叶子节点均在最后一层或者倒数第二层
- 且最后一层的节点左连续，倒数第二层的节点右连续
  
  则称该二叉树为完全二叉树
【民间定义】: 若一个树的深度为L,则从0~L - 1层位满层，最后一层可能但不为满层，但一定是左连续的

二叉树的遍历

前序遍历

基本概念：遍历顺序：根 -> 左 -> 右

public void preorderTraversal(Node node) {
		// node -> left -> right
		if(node.left == null && node.right == null) {
			System.out.println(node);
			return;
		}
		else {
			System.out.println(node); 
			if(node.left != null)preorderTraversal(node.left);
			if(node.right != null)preorderTraversal(node.right);
		}
	}

中序遍历

基本概念：遍历顺序：左-> 根 -> 右

public void inorderTraversal(Node node) {
		// left -> node -> right
		if(node.left == null && node.right == null) {
			System.out.println(node);
			return;
		}
		else {
			
			if(node.left != null)inorderTraversal(node.left);
			System.out.println(node);
			if(node.right != null)inorderTraversal(node.right);
		}
		
	}

后续遍历

基本概念：遍历顺序: 左 -> 右 -> 根

public void subsequentTraversal(Node node) {
		// left -> right -> node
		if(node.left == null && node.right == null) {
			System.out.println(node);
			return;
		}
		else {
			
			if(node.left != null)subsequentTraversal(node.left);
			if(node.right != null)subsequentTraversal(node.right);
			System.out.println(node);
		}
		
	}

顺序存储二叉树

基本原理：遍历数组时可以以遍历二叉树的方式【前序，中序，后序】的方式进行遍历
顺序存储二叉树特点【n表示数组下标】：
- 顺序存储二叉树一般只考虑完全二叉树
- 第n个元素的左子节点位2 * n + 1
- 第n个元素的右子节点位2 * n + 2
- 第n个元素的父节点位 Integer[（n - 1） / 2]

```java public void travelArr(int arr[],int turn) { //数组的树形遍历【只支持完全二叉树】

          CompTree tree = new CompTree(arr);
          switch(turn) {
          case 1:tree.preorder(0);break;
          case 2:tree.inorder(0);break;
          case 3:tree.subsequent(0);break;

          }
      }

      class CompTree{
          public CompTree(int arr[]) {
              // TODO Auto-generated constructor stub
              this.arr = arr;
          }
          int arr[];

          public void preorder(int index) {
              System.out.println(arr[index]);
              int left = 2 * index + 1;
              int right = 2 * index + 2;
              if(left < arr.length)preorder(left);
              if(right < arr.length)preorder(right);
          }

          public void inorder(int index) {

              int left = 2 * index + 1;
              int right = 2 * index + 2;
              if(left < arr.length)inorder(left);
              System.out.println(arr[index]);
              if(right < arr.length)inorder(right);
          }

          public void subsequent(int index) {
              int left = 2 * index + 1;
              int right = 2 * index + 2;
              if(left < arr.length)subsequent(left);
              if(right < arr.length)subsequent(right);
              System.out.println(arr[index]);
          }
      }


  

- [ ] 应用场景：**堆排序**





##### 线索二叉树

- [ ] 基本介绍：

  - 由于在原本的树中，有些节点的**空指针无法使用**，即浪费了许多空间

  - 使用线索二叉树可以充分利用各个节点的左右指针，让各个节点指向自己的前后节点

  - 对于最初的二叉树，若有n个节点，则一定有**n + 1的空指针域**

    > n个节点含有2 * n个指针，有n - 1个节点【即除去root】都有一个指针指向该节点。
    >
    > 所以，空节点个数 = (2 * n) - (n - 1) = n + 1

  - 利用空指针域指向某种遍历顺序下的前期和后继（**这种附加的指针称为线索**）

  - 根据线索的种类不同分为：前序线索二叉树，中序线索二叉树，后续线索二叉树
  
- [ ] 对于线索化后的二叉树：

  - 左指针可能指向左子树也可能指向前驱节点
  - 右指针可能指向右子树也可能指向后继节点
  - 所以需要额外设置一个变量用来表明其指针指向的是子树还是前/后驱节点

- [ ] 构造线索注意：

  - 对于每一个node，既是上一个节点的后继，又是下一个节点的前驱，因此，对于操作每一个节点是，将每一个node都当作中间节点来判断，且均需要考虑PreNode,和该节点的LeftNode，操作每一个节点时，都不考虑此次节点的right，因为右指针指向的是后继，递归的操作后继节点时，将该节点当作pre来对待即可

- [ ] 遍历线索二叉树注意：

  - 不可以使用原本的递归方法进行遍历【由于原本的空指针成为了线索，若递归遍历会造成死循环】
  - 使用线索化后，依然会有剩余的指针
    1. 对于前序线索化，会空出一个尾指针
    2. 对于中序线索化会空出一个头指针和一个尾指针
    3. 对于后续线索化会空出一个头指针
  - 空出的指针是遍历是结束的标志

- [ ] 这里只强调**前序线索化**和**中序线索化**【对于后续线索化太鸡儿麻烦，且需要额外的空间存父指针】

- [ ] ![](/img/picLib/preThreaded.png)

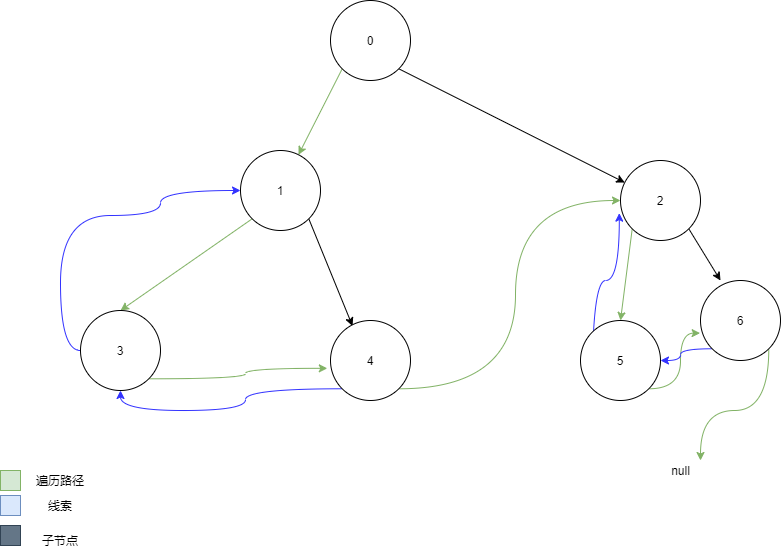
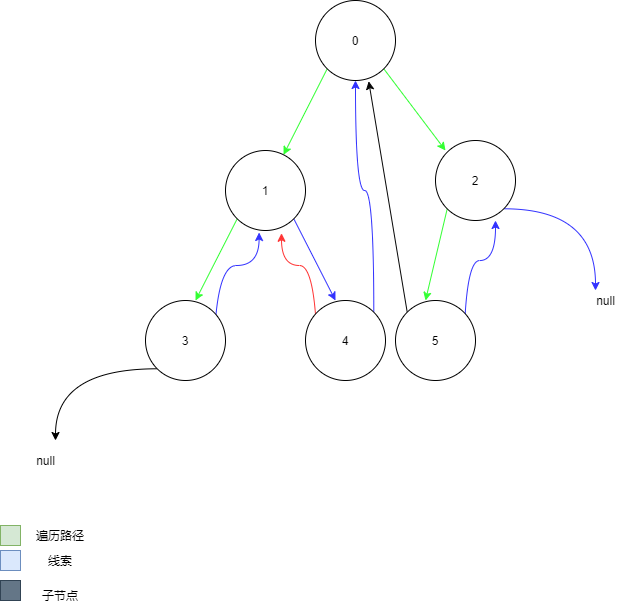
  ![Inthreaded](/img/picLib/Inthreaded.png)

- [ ] ```java
  	public boolean threaded = false;
  	
  	public void treeToThreaded(int turn) {
  		this.threaded = true;
  		ThreadedBinTree binTree = new ThreadedBinTree();
  		switch(turn) {
  		case 1:binTree.preThreadedTree(this.root);break;
  		case 2:binTree.inThreadTree(this.root);break;
  		case 3:binTree.subThreadTree(this.root);break;	
  		
  		}
  		
  	}
  	
  	
  	class ThreadedBinTree{
  		
  		private Node pre = null;
  		
  		public void preThreadedTree(Node node) {
  			if(node == null)return;
  			else {
  				if(node.left == null) {
  					node.left = pre;
  					node.lThread = true;
  				}
  				if(pre != null && pre.right == null) {
  					pre.right = node;
  					pre.rThread = true;
  				}
  				pre = node;
  				
  				
  				if(node.left != null && !node.lThread)this.preThreadedTree(node.left);
  				if(node.right != null && node.left != node.right)this.preThreadedTree(node.right);
  				
  			}
  			
  		}
  		
  		public void inThreadTree(Node node) {
  			if(node == null)return;
  			else {
  				if(node.left != null)this.inThreadTree(node.left);
  				
  				if(node.left == null) {
  					node.lThread = true;
  					node.left = pre;
  				}
  				
  				if(pre != null && pre.right == null) {
  					pre.right = node;
  					pre.rThread = true;
  				}
  					
  				pre = node;
  				
  				if(node.right != null)this.inThreadTree(node.right);
  				
  				
  			}
  		}
  		
  		
  		public void preTraver(Node node) {
  			while(node != null) {
  				while(!node.lThread) {
  					System.out.println(node);
  					node = node.left;
  				}
  				System.out.println(node);
  				node = node.right;
  				while(node != null && node.rThread) {
  					System.out.println(node);
  					node = node.right;
  				}
  				
  				
  			}
  			
  		}
  		
  		public void inTraversal(Node node) {
  			while(node != null) {
  				while(!node.lThread)node = node.left;
  				System.out.println(node);
  				while(node.rThread) {
  					node = node.right;
  					System.out.println(node);
  				}
  				node = node.right;
  			}
  			
  		}
  }

堆和堆排序

基本介绍：
- 堆排序是一种排序算法，其最快，最坏，平均时间复杂度均为O（n * logn）
- 堆排序也为不稳定排序
- 堆【前提条件是堆是一个完全二叉树】：
  
  堆是具有以下性质的完全二叉树：
  1. 每个节点的值都大于或等于其左右子节点的值，称为大顶堆
  2. 每个节点的值都小于或等于其左右子节点的值，称为小顶对
  3. 对左右子节点的值没有数值上的要求
堆排序思想和步骤：
- 用数组模拟完全二叉树
- 将待排序序列构建成一个大顶堆，最大值即根节点
- 将其与末尾元素交换，此时末尾元素即最大值
- 然后将剩余的n - 1个元素构建成大顶堆
- 重复上述步骤，直到构建称有序序列
分类：
- 升序构建小顶堆
- 降序构建大顶堆
操作注意：
- 首先找到第一个非叶子节点即 pos = (arr.length - 1) / 2
- 从第一个非叶子节点向前直到根节点【在数组中表示成从pos 到 0】依次取max(left,right,node.value)的最大值
- 遍历一遍得到当前数组的最大值，剔除（与尾元素交换）
- 直到数组的长度为0
堆排序实现既可以使用递归也可以使用非递归方法【此处采用了非递归方法】

```java package Tree;

import java.util.Arrays;

import org.junit.jupiter.api.Test;

public class HeapSort { @Test public void test() { int arr[] = {1,2,6,5,2,1,4,9,7,8}; Heap heap = new Heap(arr); heap.heapSort(true); System.out.println(Arrays.toString(heap.sortArr)); }

}

class Heap{ public int arr[]; public int sortArr[]; static final int maxNum = 65535;

public Heap(int arr[]) { // TODO Auto-generated constructor stub this.arr = arr; this.sortArr = new int[arr.length]; }

public void swapSmall(int pos,int pos1,int pos2,int length) { int v = arr[pos]; int v1 = this.maxNum; int v2 = this.maxNum; if(pos1 <= length)v1 = arr[pos1]; if(pos2 <= length)v2 = arr[pos2];

  if(v1 < v2 && v1 < v) {
      int temp = arr[pos];
      arr[pos] = arr[pos1];
      arr[pos1] = temp;
  }
  else if(v2 < v1 && v2 < v){
      int temp = arr[pos];
      arr[pos] = arr[pos2];
      arr[pos2] = temp;
  }

}

public void swapBig(int pos,int pos1,int pos2,int length) { int v = arr[pos]; int v1 = 0; int v2 = 0; if(pos1 <= length)v1 = arr[pos1]; if(pos2 <= length)v2 = arr[pos2];

  if(v1 > v2 && v1 > v) {
      int temp = arr[pos];
      arr[pos] = arr[pos1];
      arr[pos1] = temp;
  }
  else if(v2 > v1 && v2 > v){
      int temp = arr[pos];
      arr[pos] = arr[pos2];
      arr[pos2] = temp;
  }

}

public void heapSort(boolean turn) { if(turn) { int length = arr.length - 1; int index = 0; while(length >= 0) { int point = (length - 1)/2; for(int i = point;i >= 0;i--) this.swapSmall(i,2 * i + 1,2 * i + 2,length);

          sortArr[index++] = arr[0];
          arr[0] = arr[length];
          length--;
      }
  }
  else {
      int length = arr.length - 1;
      int index = 0;
      while(length >= 0) {
          int point = (length / 2) - 1;
          for(int i = point;i >= 0;i--)
              this.swapBig(i,2 * i + 1,2 * i + 2,length);

          sortArr[index++] = arr[0];
          arr[0] = arr[length];
          length--;
      }
  }

  this.arr = this.sortArr;

}





##### 通过堆排序实现优先队列

- [ ] 思路：Compareable接口 + 堆排序【虽然java已经有现成的TreeMap进行优先级的排序且底层的RBTree效率更高，写优先队列只是跟好的理解堆排序的思想】
  - add进行建堆，将node插入完全二叉树的可插入位置，即数组的最后一个位置
  - add后进行动态的维护堆
  - pop将最后一个元素调到第一个并将数组长度-1，即arr[0] = arr[length--],再进行堆得的维护

- [ ] ```java
  package Tree;
  
  import java.lang.reflect.Array;
  import java.util.Arrays;
  import java.util.TreeMap;
  
  public class PriorityQueue<E> {
  	private E arr[];
  	private Class cls;
  	
  	private int length;
  	private int capicity;
  	private double coffecient;
  	
  	
  	public PriorityQueue(Class clazz) {
  		// TODO Auto-generated constructor stub
  		this.capicity = 16;
  		this.coffecient = 0.8;
  		this.length = 0;
  		this.cls = clazz;
  		
  		arr = (E[])Array.newInstance(clazz, 16);
  		
  	}
  	
  	@Override
  	public String toString() {
  		// TODO Auto-generated method stub
  		String str = "";
  		for(int i = 0;i < this.length;i++)
  			if(i == 0)str += arr[i];
  			else str += "," + arr[i];
  		return "[" + str + "]";
  	}
  	
  	private void heapSort() {
  		Heap heap = new Heap(arr);
  		this.arr = heap.adjust();
  	}
  	
  	public void add(E e) {
  		if(this.length >= (this.capicity * this.coffecient)) {
  			Arrays.copyOf(this.arr, this.capicity * 2);
  			this.capicity *= 2;
  		}
  		
  		arr[this.length++] = e;
  		this.heapSort();
  	}
  	
  	public E top() {
  		if(this.length != 0)return arr[0];
  		return null;
  	}
  	
  	
  	public int size() {
  		return this.length;
  	}
  	
  	public boolean isEmpty() {
  		if(this.length == 0)return true;
  		else return false;
  	}
  	
  	public E pop() {
  		E e = null;
  		if(this.length != 0)e = arr[0];
  		else return null;
  		
  		arr[0] = arr[this.length - 1];
  		this.length--;
  		this.heapSort();
  		
  		return e;
  		
  		
  	}
  	
  	private class Heap{
  		private E heapArr[];
  		public Heap(E arr[]) {
  			// TODO Auto-generated constructor stub
  			this.heapArr = (E[])Array.newInstance(cls, arr.length);
  		}
  		
  		
  		public void swap(int pos,int pos1,int pos2,int len) {
  		
  			Comparable node = (Comparable) arr[pos];
  			Comparable left = null;
  			Comparable right = null;
  			if(pos1 <= len)left = (Comparable) arr[pos1];
  			if(pos2 <= len)right = (Comparable) arr[pos2];
  			if(right != null) {    
  				if(left.compareTo(right) <= 0 && left.compareTo(node) <= 0 && !arr[0].equals(left)) {
  					E temp = arr[pos];
  					arr[pos] = arr[pos1];
  					arr[pos1] = temp;
  					return;
  				}
  				if(right.compareTo(left) <= 0 && right.compareTo(node) <= 0 && !arr[0].equals(right)) {
  					
  					E temp = arr[pos];
  					arr[pos] = arr[pos2];
  					arr[pos2] = temp;
  				}
  			}
  			else if(left != null && left.compareTo(node) < 0 && !arr[0].equals(left)) {
  				
  				E temp = arr[pos];
  				arr[pos] = arr[pos1];
  				arr[pos1] = temp;
  			}
  			
  		
  			
  		}
  		
  		public E[] adjust() {
  			int len = length - 1;
  			int index = 0;
  			while(len >= 0) {
  				int point = (len - 1) / 2;
  				for(int i = point;i >= 0;i--) 
  					swap(i,i * 2 + 1,i * 2 + 2,len);
  				this.heapArr[index++] = arr[0];
  				arr[0] = arr[len];
  				len--;
  			}
  			return this.heapArr;
  		}
  		
  	}
  	
  	
  
  }

哈夫曼树

基本概念

HuffmanTree:
- 给定n个值为n个叶子的权值，构造一棵二叉树，若二叉树的带权路径权值【wpl】为最小,则称为最优二叉树，即哈夫曼树
- 即使得生成的树权值较大的离root较劲，小的离得较远
相关概念
- 路径和路径长度：从根节点到达其子节点的通路称为路径，通路的个数为路径长度，从root到达叶节点的长度为L - 1
- 节点的带权路径长度：路径 * 权值 = WPL
- 树的带权路径长度：所有节点的带权路径长度之和即Sum(WPLi) 【i = 1,2,...n】

```java class HuffmanTree{ public HuffmanNode root = null; public ArrayList list = new ArrayList<>();

public HuffmanTree(int arr[]) { // TODO Auto-generated constructor stub for(Integer w : arr) list.add(new HuffmanNode(w)); Collections.sort(list); this.constrHuffman(); }

public void preTravel(HuffmanNode node) {

  System.out.println(node);
  if(node.left != null)this.preTravel(node.left);
  if(node.right != null)this.preTravel(node.right);

}

public void constrHuffman() { while(!list.isEmpty()) { HuffmanNode node1 = list.get(0); list.remove(0); HuffmanNode node2 = null; if(!list.isEmpty()) { node2 = list.get(0); list.remove(0); } if(node2 == null) { list.add(node1); break; }

      HuffmanNode node = new HuffmanNode(node1.weight + node2.weight);
      node.left = node1;
      node.right = node2;
      list.add(node);
      Collections.sort(list);

  }

  this.root = list.get(0);

}

} class HuffmanNode implements Comparable{ int weight; public HuffmanNode left; public HuffmanNode right;

public HuffmanNode(int weight) { // TODO Auto-generated constructor stub this.weight = weight; }

@Override public int compareTo(Object o) { // TODO Auto-generated method stub HuffmanNode node = (HuffmanNode)o; if(this.weight < node.weight)return -1; else if(this.weight > node.weight)return 1; else return 0; }

@Override public int hashCode() { final int prime = 31; int result = 1; result = prime * result + weight; return result; }

@Override public boolean equals(Object obj) { if (this == obj) return true; if (obj == null) return false; if (getClass() != obj.getClass()) return false; HuffmanNode other = (HuffmanNode) obj; if (weight != other.weight) return false; return true; }

@Override public String toString() { // TODO Auto-generated method stub return weight + ""; }

}


  

##### HuffmanCode（赫夫曼编码）

- [ ] 哈夫曼编码广泛用于**数据的压缩**，一般数据的压缩程度可以达到20% ~ 90%
- [ ] 哈夫曼编码是可变字长编码的一种（VLC）
- [ ] 按照压缩的原理：在传输过程中，出现次数多的使用较长的编码，出现次数少的，使用较短长度的编码
- [ ] **哈夫曼编码遵循前缀码原则，即任何一个元素的编码都不会为其他元素编码的前缀，保证了编码无二义性**
- [ ] 不同操作建立的哈夫曼树可能不同但是平均权值是一定相同的

###### 赫夫曼压缩

- [ ] 利用Huffman编码并持久化存储

- [ ] ```java
  	
  	private byte[] getByteStream(String text) {
  		String coded = this.text2Code(text);
  		
  		int len = 0;
  		if(coded.length() % 8 == 0)len = coded.length() / 8;
  		else len = (coded.length() / 8) + 1;
  		
  		byte bytes[] = new byte[len];
  		
  		int index = 0;
  		for(int i = 0;i < coded.length();i += 8) {
  			String strByte = null;
  			if(i + 8 < coded.length())strByte = coded.substring(i,i + 8);
  			else strByte = coded.substring(i);
  			bytes[index++] = (byte)Integer.parseInt(strByte,2);
  		}
  		
  		return bytes;
  	}
  	
  	
  	public void save(String path,byte[] bytes) {
  		FileOutputStream fos = null;
  		BufferedOutputStream bfos = null;
  		
  		try {
  			fos = new FileOutputStream(path);
  			bfos = new BufferedOutputStream(fos);
  			try {
  				bfos.write(bytes);
  				bfos.flush();
  			} catch (IOException e) {
  				// TODO Auto-generated catch block
  				e.printStackTrace();
  			}
  			
  			
  		} catch (FileNotFoundException e) {
  			// TODO Auto-generated catch block
  			e.printStackTrace();
  		}finally {
  			try {
  				fos.close();
  				bfos.close();
  			} catch (IOException e) {
  				// TODO Auto-generated catch block
  				e.printStackTrace();
  			}
  		}
  		
  	}
  	
  	public void zip(String text,String path) {
  		byte bytes[] = this.getByteStream(text);
  		this.save(path, bytes);
  		System.out.println("zip sucessfully!");
  		
  	}

赫夫曼解压

在解压时需要进行补位，不能直接对字节类型进行截取【正数位数需要补位】

```java public String decoded(String path) throws IOException { String coded = this.unZip(path); return this.code2Text(coded);

}

private int getFileSize(String path) { File file = new File(path); if(file.exists())return (int) file.length(); else return -1; }

private String unZip(String path) throws IOException { FileInputStream fis = null; BufferedInputStream bfis = null; String coded = "";

  int fileSize  =this.getFileSize(path);
  byte[] bytes = new byte[fileSize];

  try {
      fis = new FileInputStream(path);
      bfis = new BufferedInputStream(fis);
      int len = 0;
      while((len = bfis.read(bytes)) != -1);

  } catch (FileNotFoundException e) {
      // TODO Auto-generated catch block
      e.printStackTrace();
  }finally {
      fis.close();
      bfis.close();
  }


  for(int i = 0;i < bytes.length;i++) {
      int temp = bytes[i];
      if(i != bytes.length - 1) {
          temp |= 256;
          String str = Integer.toBinaryString(temp);
          coded += str.substring(str.length() - 8); // 由于获得是补码因此不可以直接使用str，需要截取后8位
      }
      else {
          String str = Integer.toBinaryString(temp); // 最后一个Byte可能不满一个字节因此不需要进行补位
          coded += str;
      }
  }


  return coded;

}


  

######  赫夫曼文件压缩与解压

- [ ] 基本原理：

  - 通过对文件的二进制文件读取，将二进制的的整数型作为关键词进行哈夫曼编码，将编码后的文件和解码树一并存放
  - 读取时先读取编码文件，再读取解码树

- [ ] ```java
  package Tree.Huffman;
  
  import java.io.FileInputStream;
  import java.io.FileOutputStream;
  import java.io.IOException;
  import java.io.ObjectInputStream;
  import java.io.ObjectOutputStream;
  import java.util.ArrayList;
  import java.util.HashMap;
  
  import Tree.PriorityQueue;
  
  public class HuffmanCoder{
  	
  	private HuffmanTree huffTree = null;
  	public HashMap<Byte,String> codeMap = new HashMap<Byte, String>();// key -> 源码 value -> huffCode
  	
  	private ArrayList<HuffmanNode> nodeList = new ArrayList();
  	
  	public HuffmanCoder() {
  		// TODO Auto-generated constructor stub
  	}
  	
  	
  	
  	private PriorityQueue<HuffmanNode> getHuffmanQueue(byte[] sCodes) { // 通过对源文件的编码获得新的编码
  		PriorityQueue<HuffmanNode> queue = new PriorityQueue<HuffmanNode>(HuffmanNode.class);
  		HashMap<Byte,Integer> cntMap = new HashMap(); 
  		
  		for(Byte code : sCodes) {
  			if(cntMap.containsKey(code)) {
  				int cnt = cntMap.get(code);
  				cntMap.put(code, cnt++);
  			}
  			else cntMap.put(code, 1);
  		}
  		
  		
  		for(Byte b : cntMap.keySet()) {
  			int cnt = cntMap.get(b);
  			HuffmanNode node = new HuffmanNode(String.valueOf((int)b));
  			queue.add(node);
  		}
  		
  		return queue;
  		
  		
  	}
  	
  	
  	private byte[] restrore(String code) {
  		HuffmanNode node = this.huffTree.root;
  		String reCode = "";
  		
  		for (int i = 0; i < code.length(); i++) {
  			String c = code.charAt(i) + "";
  			if(c.equals("0"))node = node.left;
  			else node = node.right;
  			if(node.left == null && node.right == null) {
  				reCode += node.data;
  				node = this.huffTree.root;
  			}
  		}
  		
  		int len = (reCode.length() + 7) /  8; 
  		byte[] bytes = new byte[len];
  		int index = 0;
  		for(int i = 0;i < reCode.length();i++) {
  			if(i != reCode.length() - 1) {
  				String str = reCode.substring(i,i + 8);
  				bytes[index++] = (byte)Integer.parseInt(str,2);
  			}
  			else {
  				String str = reCode;
  				bytes[index++] = (byte)Integer.parseInt(str,2);
  			}
  		}
  		return bytes;
  		
  	}
  	
  	private byte[] primaryCode(byte[] bytes) {
  		String code = "";
  		for(int i = 0;i < bytes.length;i++) {
  			int b = bytes[i]; //由于此步骤中b自动忽略了首部的0，因此需要在后需要的步骤中进行对0的补充
  			if(i != bytes.length - 1) {
  				b |= 256; // 对0进行补位
  				String str = Integer.toBinaryString(b);
  				code += str.substring(str.length() - 8);
  				
  			}
  			else {
  				String str = Integer.toBinaryString(b);
  				code += str;
  				
  			}
  		}
  		return this.restrore(code);
  		
  	}
  	
  	
  	
  	
  	public void decoding(String srcFile,String dstFile) {
  		
  		FileInputStream fis = null;
  		ObjectInputStream ois = null;
  		FileOutputStream fos = null;
  		
  		try {
  			fis = new FileInputStream(srcFile);
  			ois = new ObjectInputStream(fis);
  			byte[] bytes = (byte[]) ois.readObject();
  			HuffmanTree tree = (HuffmanTree) ois.readObject();
  			this.huffTree = tree;
  			byte[] priBytes = this.primaryCode(bytes);
  			fos.write(priBytes);
  			
  		} catch (ClassNotFoundException | IOException e) {
  			// TODO Auto-generated catch block
  			e.printStackTrace();
  		}finally {
  			try {
  				fis.close();
  				ois.close();
  				fos.close();
  			} catch (IOException e) {
  				// TODO Auto-generated catch block
  				e.printStackTrace();
  			}
  		}
  		
  		
  		
  	}
  	
  	
  	public void encoding(HuffmanNode node,String bit) {
  		if(node.left == null && node.right == null) {
  			Byte code = (byte)Integer.parseInt(node.data);
  			codeMap.put(code, bit);
  		}
  		else {
  			if(node.left != null)this.encoding(node.left, bit + "0");
  			if(node.right != null)this.encoding(node.right, bit + "1");
  		}
  	}
  	
  	public byte[] source2Code(byte[] bytes) {
  		String huffStr = ""; // 编码后的数组
  		for(Byte b : bytes) 
  			huffStr += codeMap.get(b);
  		
  		int len = (huffStr.length() + 7) / 8;
  		byte[] codedBytes = new byte[len];
  		int index = 0;
  	
  		
  		
  		for(int i = 0;i < huffStr.length();i += 8) {
  			
  			if(i + 8 < huffStr.length())
  				codedBytes[index++] = (byte)Integer.parseInt(huffStr.substring(i,i + 8),2);
  			else codedBytes[index++] = (byte)Integer.parseInt(huffStr.substring(i),2);
  		}
  		
  		
  		return codedBytes;
  		
  		
  		
  		
  	}
  	
  	public byte[] getHuffmanCodes(byte[] bytes) {
  		
  		PriorityQueue<HuffmanNode> queue = this.getHuffmanQueue(bytes);
  		this.huffTree = new HuffmanTree();
  		this.huffTree.constrHuffman(queue);
  		
  		if(this.huffTree.root.left != null)this.encoding(this.huffTree.root.left, "0");
  		if(this.huffTree.root.right != null)this.encoding(this.huffTree.root.right, "1");
  		
  		return this.source2Code(bytes);
  		
  	}
  	
  	
  	public void zipFile(String srcFile,String dstFile) {
  		
  		FileInputStream fis = null;
  		FileOutputStream fos = null;
  		ObjectOutputStream oos = null;
  		
  		
  		try {
  			fis = new FileInputStream(srcFile);
  			byte[] bytes = new byte[fis.available()];
  			fis.read(bytes);
  			byte[] huffmanCodes = this.getHuffmanCodes(bytes);
  			fos = new FileOutputStream(dstFile);
  			
  			oos = new ObjectOutputStream(fos);
  			oos.writeObject(huffmanCodes);
  			oos.writeObject(this.huffTree);
  			
  		} catch (IOException e) {
  			// TODO Auto-generated catch block
  			e.printStackTrace();
  		}finally {
  			try {
  				fis.close();
  				fos.close();
  				oos.close();
  			} catch (IOException e) {
  				// TODO Auto-generated catch block
  				e.printStackTrace();
  			}
  		}
  		
  		
  		
  	}
  	
  	
  	
  	
  	
  	
  }

二叉排列树【二叉搜索树】

基本概念

二叉排序树要求左子树值小于当前的节点，右子树的值大于当前的节点
由于二叉排列树的特点：即左< 中 < 右，因此通过中序遍历可以得到有序的从小到大的序列
排列数最基本特点：
- 最小值一定在最左边
- 最大值一定在最右边

二叉排列树的创建和中序遍历

```java private void insertNode(BinaryNode node,BinaryNode temp) { if(temp.compareTo(node) >= 0) { if(temp.left != null) this.insertNode(node, this.root.left); else temp.left = node; } else { if(temp.right != null) this.insertNode(node, this.root.right); else temp.right = node; } }

public void insert(E data) { BinaryNode node = new BinaryNode(data); if(this.root == null) { root = new BinaryNode(data); return; } else { if(this.root.compareTo(node) >= 0) { if(this.root.left != null) this.insertNode(node, this.root.left); else this.root.left = node; return; } else { if(this.root.right != null) this.insertNode(node, this.root.right); else this.root.right = node; return; } }

}

private void inOrderTra(BinaryNode node) { if(node.left == null && node.right == null) { System.out.println(node); return; } else { if(node.left != null)this.inOrderTra(node.left); System.out.println(node); if(node.right != null)this.inOrderTra(node.right); } }

public void traversal() { this.inOrderTra(this.root); }


  



##### 二叉排列树的删除

- [ ] 对于二叉排列树的删除：

  - 若删除的是叶子节点：直接通过Parent节点进行删除

  - 若删除的节点仅有左节点或右节点：则让子节点代替当前节点

  - 若删除的节点左右节点均存在：

    1. 找到左子树最大的
    2. 或者找到右子树最小的

    使用找到的节点代替当前节点

- [ ] ```java
  public void deleteNode(BinaryNode<E> pre,BinaryNode<E> node,int type) {
  		int pos = 0;
  		if(node == pre.left)pos = 1;
  		else pos = -1;
  		
  		switch(type) {
  		case 0:{
  			if(pos == 1)pre.left = null;
  			else pre.right = null;
  		};break;
  		case 1:{
  			if(pos == 1) 
  				pre.left = node.right;
  			else pre.right = node.right;
  			
  		};break;
  		case 2:{
  			if(pos == 1)
  				pre.left = node.left;
  			else pre.right = node.left;
  			
  		};break;
  		case 3:{
  			BinaryNode<E> temp = node.left;
  			BinaryNode<E> tempPre = node;
  			while(temp.right != null) {
  				tempPre = temp;
  				temp = temp.right;
  			}
  			node.data = temp.data;
  			tempPre.right = null;
  		}
  			
  		
  		}
  	}
  	
  	private int deleteType(BinaryNode<E> node) {
  		if(node.left != null && node.right != null)return 3;
  		else if(node.left != null && node.right == null)return 2;
  		else if(node.right != null && node.left == null)return 1;
  		else return 0;
  		
  	}
  	public void delete(E data) {
  		if(this.root == null)return;
  		else {
  			if(this.root.data.equals(data)){
  				if(this.root.left != null) {
  					BinaryNode<E>  node = this.root.left;
  					while(node.right != null)node = node.right;
  					BinaryNode<E> reNode = this.root.left;
  					while(reNode.right != null && reNode.right != node)
  						reNode = reNode.right;
  					this.root = node;
  					reNode.right = null;
  				}
  				else if(this.root.right != null){
  					BinaryNode<E>  node = this.root.right;
  					while(node.left != null)node = node.left;
  					BinaryNode<E> reNode = this.root.right;
  					while(reNode.left != null && reNode.left != node)
  						reNode = reNode.left;
  					this.root = node;
  					reNode.left = null;
  				}
  				else this.root = null;
  			}
  			else {		
  				BinaryNode<E> temp = null;
  				BinaryNode<E> pre = this.root;
  				BinaryNode<E> node = new BinaryNode<E>(data);
  				int comp = pre.compareTo(node);
  				if(comp > 0)temp = pre.left;
  				else temp = pre.right;
  				while(temp != null) {
  					comp = temp.compareTo(node);
  					if(comp > 0) {
  						pre = temp;
  						temp = temp.left;
  					}
  					else if(comp < 0) {
  						pre = temp;
  						temp = temp.right;
  					}
  					else {
  						this.deleteNode(pre, temp, this.deleteType(temp));
  						return;
  					}
  				}
  				System.out.println("not find");
  			}
  		}
  	}

基本删除思路很简单，但是需要注意对于root的处理，因为root没有preNode，因此对于root需要单独判断

二叉平衡树

基本概念

对于一般的二叉排序树，如果插入时是有序的数列则会长成

即生成一个链表形式，而不是树的形式，即树退化成了链表【对于插入和删除没有影响，但是查询速度为链表的查询速度】

AVL特点：
- 平衡二叉树树为空树，或者左右两个子树的高度差不超过1
- 平衡二叉树左右子树也均为平衡二叉树
平衡二叉树的常用实现方法：
- 红黑树（RBTree）
- AVL
- 替罪羊树
- Treap
- 伸展树
旋转概念：
- 左旋右长
- 右旋左长

AVL左旋转

若插入右子树使得平衡二叉树失去平衡则需要进行左旋转
基本步骤：
- 创建一个新的节点（newNode），值等于根节点(root)的值
- 新节点（newNode）的左子树指向根节点(root)的左子树
- 新节点（newNode）的右子树指向根节点(root)右子树的左子树
- 根节点(root)的值替换为根节点(root)右子树的值
- 根节点(root)的右子树指向根节点(root)右子树的右子树
- 根节点(root)的左子树指向新节点（newNode）
通过以上步骤完成了左子树深度+1，右子树深度-1

```java private void leftRotation() { System.out.println("left avl"); BinaryNode node = new BinaryNode((E) this.tree.root.data); node.left = this.tree.root.left; node.right = this.tree.root.right.left;

      this.tree.root.data = this.tree.root.right.data;
      this.tree.root.left = node;
      this.tree.root.right = this.tree.root.right.right;
  }












##### AVL右旋转

- [ ] 将插入后不平衡树向右倾斜

- [ ] 基本步骤【与左旋转对称】：

  - 创建一个新的节点，并赋值为根节点的值
  - 当前节点的右子树指向根节点的右子树
  - 当前节点的左左子树指向根节点左子树的右子树
  - 根节点的值赋值为根节点左子树的左子树
  - 根节点的左子树指向根节点左子树的左子树
  - 根节点的右子树指向新的节点

- [ ] ![](/img/picLib/avlRight.png)

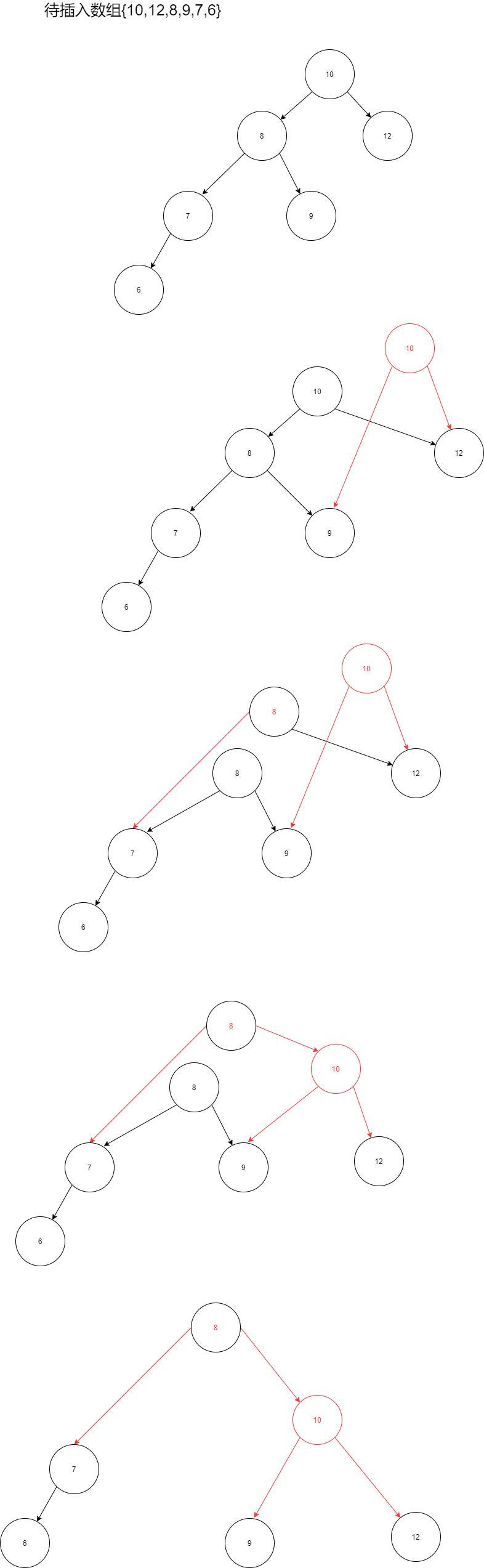
- [ ] ```java
  
    	private void rightRotation(BinaryNode<E> node) {
    		this.legalzationChild(false, node.left);
    		
    		BinaryNode<E> temp = new BinaryNode<E>((E) node.data);
    		temp.right = node.right;
    		temp.left = node.left.right;
    		
    		node.data = node.left.data;
    		node.left = node.left.left;
    		node.right = temp;
    	}

AVL双旋转

对于某些数组再对根节点进行单旋转之前需要对其相应的子树进行判断是否符合单旋转，若不符合则需要进行双旋转，使子树合法，再进一步对根节点进行旋转
旋转子树合法判断：
- 若对节点（Node1）进行左旋转，需要该节点(Node1)的右子树(Node2)的左子树深度小于该右子树(Node2)的右子树深度
- 若对节点(Node1)进行右旋转，需要该节点(Node1)的左子树(Node2)的右子树深度小于该左子树(Node2)的左子树深度

```java

private void legalzationChild(boolean left,BinaryNode node) { if(left) { int lDepth = 0; int rDepth = 0; if(node.left != null)lDepth = this.getDepth(node.left); if(node.right != null)rDepth = this.getDepth(node.right); if(lDepth > rDepth)this.rightRotation(node); } else { int lDepth = 0; int rDepth = 0; if(node.left != null)lDepth = this.getDepth(node.left); if(node.right != null)rDepth = this.getDepth(node.right); if(rDepth > lDepth)this.leftRotation(node); }

} private void rightRotation(BinaryNode node) { this.legalzationChild(false, node.left);

  BinaryNode<E> temp = new BinaryNode<E>((E) node.data);
  temp.right = node.right;
  temp.left = node.left.right;

  node.data = node.left.data;
  node.left = node.left.left;
  node.right = temp;

}

private void leftRotation(BinaryNode node) {

  this.legalzationChild(true, node.right);

  BinaryNode<E> temp = new BinaryNode<E>((E) node.data);
  temp.left = node.left;
  temp.right = node.right.left;

  node.data = node.right.data;
  node.left = temp;
  node.right = node.right.right;

}


  

#### 红黑树







#### 多路查找树

##### 二叉树与B树

- [ ] 二叉树的局限性：
  - 使用二叉树需要加载到内存，当二叉树的节点少时内存可以容忍，当二叉树结点个数较多时内存无法忍受
  - 当结点个数过多时：
    1. 内存消耗大
    2. 多次进行I/O操作时速度慢
    3. 树的高度过高
- [ ] 多叉树：
  - 当允许结点的个数大于2时，此时树升级为多叉树（Multiway Tree）
  - 多叉树的优势：通过重新组织结点，从而减少树的高度，提高查找效率
  - 当一个结点有两个子节点则此节点为2结点，若有3个子节点则为3结点
  - 通过多叉树可以对**大量**的数据进行快速查询
- [ ] B树的基本介绍：
  - 相关概念：
    1. 结点的度：结点子树的个数
    2. 树的度：所有结点中结点度最大的即为树的度
  - B树即为一种多叉树
  - B树及其延伸的树均为平衡树
  - B树B+树适用于数据库管理系统的表的索引





##### 2-3树

- [ ] 基本概念：2-3树是一种就简单的**B**树
- [ ] 结构特点：
  - 2-3树的所有叶子结点均在同一层**（所有B树均需要满足的特点）**
  - 二节点要么没有子节点，要么有两个子节点
  - 三节点要么没有子节点，要么有3个子节点
  - 2-3树是由二节点和三节点构成的树
- [ ] ![](/img/picLib/23t.png)







##### B树/B+树/B*树

- [ ] 误区：B树即B-Tree【**B-树就是B树**】
- [ ] 基本概念：
  - B树的阶：即B树最多子节点的个数（2-3树的阶为3，2-3-4树的阶为4）
- [ ] B+树基本概念：
  - B+树的所有信息存放在叶子结点而非叶子结点中不在存放信息
  - 所有关键词都存放在叶子结点的链表中，在链表中的索引即【稠密索引】
  - 非叶子结点的索引即【稀疏索引】
  - B+树叶子结点的链表连接在一起
- [ ] B*树：
  - 在非根非叶子结点之间添加指针使得兄弟非叶子结点之间可以互相连接









### 图

#### 基本介绍

- [ ] 为什么需要图：
  - 线性表局限于一个前驱和一个后继【一对一】
  - 树局限于一个前驱和多个后继【一对多】
  - 当需要多对多的关系时需要图的结构
- [ ] 相关概念：
  - 顶点(Vertex)
  - 边(edge)
  - 路径
  - 无向图
  - 有向图
  - 带权图
- [ ] 图的表示方式：
  - 邻接矩阵【二维数组】
  - 邻接表【数组 + 链表】



#### 图的创建即遍历

##### 邻接表【dfs + bfs】

```java
package Graph;

import java.util.ArrayList;

public class AdajacentMatrix{
	private int cnt =  0;
	private boolean matrix[][];
	private boolean directed;
	public AdajacentMatrix(int cnt,boolean dire) {
		// TODO Auto-generated constructor stub
		this.cnt = cnt;
		this.matrix = new boolean[cnt][cnt];
		for(int i = 0;i < cnt;i++)this.matrix[i][i] = true;
		
		this.directed = dire;
	}
	
	public void addEdge(int pos1,int pos2) {
		if(directed)
			matrix[pos1][pos2] = true;
		else {
			matrix[pos1][pos2] = true;
			matrix[pos2][pos1] = true;
		}
	}
	
	public void deleteEdge(int pos1,int pos2) {
		if(directed)
			matrix[pos1][pos2] = false;
		else {
			matrix[pos1][pos2] = false;
			matrix[pos2][pos1] = false;
		}
	}
	
	
	public void bfs(ArrayList queue,boolean vis[]) {
		// TODO Auto-generated method stub
		
		while(!queue.isEmpty()) {
			int vertex = (int) queue.get(0);
			queue.remove(0);
			
			for(int i = 0;i < this.cnt;i++)
				if(this.matrix[vertex][i] && !vis[i]) {
					System.out.println(i);
					queue.add(i);
					vis[i] = true;
				}
		}
		
		
		
		
	}
	
	public void dfs(int vertex,boolean vis[]) {
		// TODO Auto-generated method stub
		vis[vertex] = true;
		System.out.println(vertex);
		for(int i = 0;i < this.cnt;i++)
			if(this.matrix[vertex][i] && !vis[i]) 
				this.dfs(i, vis);
			
				
	}
	
	public void traversal(boolean dfirst) {
		boolean vis[] = new boolean[this.cnt];
		if(dfirst) {
			for(int i = 0;i < this.cnt;i++)
				if(!vis[i])this.dfs(i,vis);
		}
		else {
			ArrayList queue = new ArrayList();
			for(int i = 0;i < this.cnt;i++)
				if(!vis[i]) {
					System.out.println(i);
					vis[i] = true;
					queue.add(i);
					this.bfs(queue,vis);
				}
		}
	}

	
	
	

}

邻接矩阵【dfs + bfs】

package Graph;

import java.util.ArrayList;
import java.util.HashMap;

public class AdajacentTable {
	
	private HashMap<Object,ArrayList<Object>> table = null;
	private boolean dire;
	
	
	public void addEdge(int pos1, int pos2) {
		// TODO Auto-generated method stub
		if(this.dire) {
			if(!this.table.containsKey(pos1))table.put(pos1, new ArrayList<>());
			if(table.get(pos1).contains(pos2))return;
			else table.get(pos1).add(pos2);
		}
		else {
			if(!this.table.containsKey(pos1))table.put(pos1, new ArrayList<>());
			if(!this.table.containsKey(pos2))table.put(pos2, new ArrayList<>());
			if(table.get(pos1).contains(pos2))return;
			else table.get(pos1).add(pos2);
			
			if(table.get(pos2).contains(pos1))return;
			else table.get(pos2).add(pos1);
		}
	}
	
	public AdajacentTable(boolean dire) {
		// TODO Auto-generated constructor stub
		this.dire = dire;
		this.table = new HashMap<Object, ArrayList<Object>>();
		
	}
	
	public void dfs(int vertex, ArrayList vis) {
		// TODO Auto-generated method stub
		vis.add(vertex);
		System.out.println(vertex);
		for(Object obj : this.table.get(vertex)) {
			if(!vis.contains(obj)) {
				this.dfs(vertex, vis);
			}
		}
		
	}
	
	public void bfs(ArrayList queue, ArrayList vis) {
		// TODO Auto-generated method stub
		while(!queue.isEmpty()) {
			int vertex = (int) queue.get(0);
			queue.remove(0);
			for(Object i : this.table.get(vertex)) {
				if(!vis.contains(i)) {
					System.out.println(i);
					vis.add(i);
					queue.add(i);
				}
			}
			
		}
	}
	
	
	public void traversal(boolean dfirst) {
		// TODO Auto-generated method stub
		ArrayList vis = new ArrayList();
		if(dfirst) {
			for(Object obj : table.keySet())
				if(!vis.contains(obj))
					this.dfs((Integer)obj, vis);
		}
		else {
			ArrayList queue = new ArrayList();
			for(Object obj : table.keySet())
				if(!vis.contains(obj)) {
					vis.add(obj);
					queue.add(obj);
					System.out.println(obj);
					this.bfs(queue, vis);
				}
					
		}
	}
}

注意点：
- 对于dfs或是bfs上锁的位置其实是相同的，均是在输出的位置进行上锁，避免了重复输出和重复遍历
- dfs采用深度优先的思想：找到 --> 上锁 --> 进入dfs
- bfs采用广度优先的思想需要配合队列适用：找到 --> 上锁 ---> 入队 ---> 等到该次循环完毕知乎堆子节点队列遍历
- 在bfs时队列候选子队列需要一直传递，当队列空时再返回call函数

并查集

基本算法

分治算法

基本概念：
- 将大问题分成若干个问题相似，但规模小的问题，小问题解合并成大问题的解
- 基本步骤：
  1. 分解
  2. 解决
  3. 合并
- 由于分治的思想和递归思想不谋而合，因此大多数的分治问题可以通过递归的方法解决

汉诺塔问题

static public void hannoi(int n,String A,String B,String C) {
		if(n == 1) {
			System.out.println(A + " ---> " + C);
		}
		else {
			hannoi(n - 1, A, C, B);
			System.out.println(A + " ---> " + C);
			hannoi(n - 1, B, A, C);
		}
		
	}

动态规划

将大问题分成规模小问题相似的小问题，通过获得小问题的最优解从而获得大问题的最优解
与分治法的区别：小问题不是相互独立的，而是相依赖的，即小问题的解需要用到更小的问题的解
0-1背包问题 / 完全背包问题

字符串匹配算法

暴力匹配

基本步骤：
- 依次遍历母串，若母串[ i ] == 子串[ 0 ]，则进行i++,j++直到母串结束或子串结束或字符不匹配
- 判断j == 子串.length - 1若是则找到返回i - j，否则未找到i = i - j + 1，j = 0
- 即只要发现匹配错误，就向前进1

```java static void violientMatch(String str1,String str2) { int j = 0; for(int i = 0;i < str1.length();i++) { if(str1.charAt(i) == str2.charAt(0)) { while(i < str1.length() - 1 && j < str2.length() - 1 && str1.charAt(i) == str2.charAt(j)) { i++; j++; } if(j != str2.length() - 1) { i = i - j + 1; j = 0; } else { System.out.println(i - j); break; } } } }


  

##### KMP

- [ ] 基本思想：

  - 根据**子串**的结构获得部分匹配表
  - 通过部分匹配表完成字符串的匹配
  - 即找到**最长公共前后缀**位置，再从该位置继续找
  - **val = next[pos] 的值表示从子串开始val个数与从pos开始向前val个数相同**
  - next数组的作用找到从头开始val个数 + 1的位置的元素与当前不相等的元素进行比较,若未找到，则继续找和此后缀最长的前缀位置替换至i - 1处，再从前缀 + 1处的元素比较

- [ ] ```java
  static public void kmpMatch(String str1,String str2) {
  		int next[] = getNext(str2);
  		int j = 0;
  		for(int i = 0;i < str1.length();i++) {
  			while(j > 0 && str2.charAt(j) != str1.charAt(i))j = next[j - 1];
  			if(str1.charAt(i) == str2.charAt(j))j++;
  			if(j == str2.length() - 1) {
  				System.out.println(i - j + 1);
  				return;
  			}
  		}
  		
  	}
  	
  	static public int[] getNext(String str) {
  		int next[] = new int[str.length()];
  		for(int i = 1,j = 0;i < str.length();i++) {
  			while(j > 0 && str.charAt(i) != str.charAt(j))j = next[j - 1];
  			if(str.charAt(i) == str.charAt(j)) {
  				i++;j++;
  			}
  			next[i] = j;
  		}
  		return next;
  	}

最小生成树

普利姆算法

基本步骤：
- 初始化选中一个结点v0,vis[v0] = true，加入结点集
- 从结点集种选中连接的边种最小的权值连接点v1，vis[v1] = true
- 重复2过程
- 只要保证新加的边的其中一点没有被选中过，就可以保证无回路生成：若加入边后有回路，当且仅当被选中的其中一点在树中，与点未被选中想违背，所以只要点没有被选中过则无回路

```java static final int minNum = 65535;

static public int prim(int map[][]) { boolean vis[] = new boolean[map.length]; HashSet set = new HashSet();

  vis[0] = true;
  set.add(0);

  int quality = 0;
  int min = minNum;



  while(set.size() != map.length) {

      int findPoint = -1;
      int outNode = -1;
      for(int i = 0;i < map.length;i++) {
          for(int j = 0;j < map.length;j++) {
              if(vis[i] && !vis[j] && map[i][j] < min) {
                  min = map[i][j];
                  findPoint = j;
                  outNode = i;
              }
          }
      }
      vis[findPoint] = true;
      quality += min;
      set.add(findPoint);
      min = minNum;
      System.out.println(outNode + " --> " + findPoint);
  }
  return quality;

}


  

##### 克鲁斯卡尔算法

- [ ] 难点：判断回路【只要结点的终点不相同则可以进行边的添加，否则不可以添加】

- [ ] ```java
  static public int getDst(int []dst,int i) {
  		while(dst[i] != -1)i = dst[i];
  		return i;
  	}
  	
  	static public int kruskal(int map[][]) {
  		int dst[] = new int[map.length];
  		for(int i = 0;i < dst.length;i++)dst[i] = -1;
  		boolean vis[] = new boolean[map.length];
  		int cnt = 0;
  		int quality = 0;
  		
  		PriorityQueue<Edge> queue = new PriorityQueue(Edge.class);
  		for(int i = 0;i < map.length;i++) {
  			for(int j = 0;j < map.length;j++)
  				if(map[i][j] < minNum)
  					queue.add(new Edge(i, j, map[i][j]));
  		}
  		
  		
  		while(cnt != map.length - 1) {
  			Edge edge = queue.pop();
  			int node1 = edge.list.get(0);
  			int node2 = edge.list.get(1);
  			int dst1 = getDst(dst, node1);
  			int dst2 = getDst(dst,node2);
  			if(dst1 != dst2) {
  				cnt++;
  				quality += edge.w;
  				dst[dst1] = dst2;
  			}
  			
  		}	
  		
  		return quality;
  	}
  class Edge implements Comparable{
  	ArrayList<Integer> list = new ArrayList();
  	int w;
  	public Edge(int node1,int node2,int w) {
  		// TODO Auto-generated constructor stub
  		this.list.add(node2);
  		this.list.add(node1);
  		
  		this.w = w;
  	}
  	
  	@Override
  	public int compareTo(Object o) {
  		// TODO Auto-generated method stub
  		Edge edge = (Edge)o;
  		if(this.w < edge.w)return -1;
  		else if(this.w == edge.w)return 0;
  		else return 1;
  		
  	}
  	@Override
  	public String toString() {
  		// TODO Auto-generated method stub
  		return this.w + "";
  	}
  }

根据回路算法。在一棵树上只有终点的值是常量C，其余均是dst均是通向终点的路径，这样保证了在一颗树上加入新的结点时，更改的一定是终点

最短路径

迪杰斯特拉算法

求出两点之间的最短路径

  static final int minNum = 65535;
static public void printPath(int arr[],int start,int temp) {
	if(temp == start) {
		System.out.println(start);
	}
	else {
		printPath(arr, start, arr[temp]);
		System.out.println(temp);
	}
}

static public int dijkstra(int map[][],int start,int end) {
	boolean vis[] = new boolean[map.length];
	int index = start;
	vis[index] = true;
	int nodeWeight[] = new int[map.length];
	for(int i = 0;i < nodeWeight.length;i++)nodeWeight[i] = minNum;
	nodeWeight[index] = 0;
	int path[] = new int[map.length];
	while(true) {
		int min = minNum;
		for(int i = 0;i < map.length;i++) 
			if(!vis[i] && nodeWeight[index] + map[index][i] < nodeWeight[i]) {
				nodeWeight[i] = nodeWeight[index] + map[index][i];
				path[i] = index;
			}
				
		int next = -1;
		for(int i = 0;i < map.length;i++)
			if(nodeWeight[i] < min && !vis[i]) {
				min = nodeWeight[i];
				index = i;
			}
		vis[index] = true;
		if(index == end)break;
		
	}
	
	printPath(path, start, end);
	return nodeWeight[end];
	
}

弗洛伊德算法

求出所有点之间的最短路径
基本原理：
- 假设已知Vi到Vk之间的最短路径为Lik,Vk到Vj之间的最短路径为Lkj
- 已知当前的Vi到Vj之间的最短路径为Lij
- 则Lij = Min(Lij,(Lik + Lkj))

```java static public void floyd(int map[][]) { int path[][] = new int[map.length][map.length]; for(int i = 0;i < map.length;i++) for(int j = 0;j < map.length;j++) path[i][j] = i;

  for(int k = 0;k < map.length;k++) {
      for(int i = 0;i < map.length;i++) {
          for(int j = 0;j < map.length;j++)
              if(map[i][k] + map[k][j] < map[i][j]) {
                  map[i][j] = map[i][k] + map[k][j];
                  path[i][j] = path[k][j];
              }
      }
  }

}

```